Многие трёхмерные геометрические формы могут быть аппроксимированы функциями Аппроксимация формы для изображений и данных XYZ, которые имеют общие параметры. Следовательно, мы сначала опишем общие для них параметры и отдельно затем перечислим особые параметры в описаниях отдельных аппроксимирующих геометрических форм.
- x0
Горизонтальное положение центра фигуры, обычно совпадает с вершиной (или самой нижней точкой для фигур с отрицательной высотой). Для периодических форм это смещение относительно начала координат одной из бесконечного множества фигур.
- y0
Вертикальное положение центра фигуры, обычно совпадает с вершиной (или самой нижней точкой для фигур с отрицательной высотой). Для периодических форм это смещение относительно начала координат одной из бесконечного множества фигур.
- z0
Высота базовой плоскости (в центре фигуры, если базовая плоскость наклонена). Следует заметить, что этот параметр может показывать 100% корреляцию с другими параметрами, относящимися к высоте, если фигура занимает всё изображение и базовая плоскость не видна.
- h
Высота фигуры по отношению к горизонтальной базовой плоскости.
- φ
Вращение в положительном направлении по отношению к основной системе координат, в которой обычно главные оси фигуры выровнены горизонтально и вертикально.
- bx
Наклон базовой плоскости в горизонтальном направлении.
- by
Наклон базовой плоскости в вертикальном направлении.
- a
Параметр анизотропии. Он равен отношению более длинной и более короткой сторон (или полуосей или других размерностей ширины) фигуры. Следовательно, одна из сторон будет равна средней ширине, умноженной на √a, а другая средней ширине, делённой на √a. Зафиксируйте его равным единице если фигура не должна растягиваться в одном направлении и сжиматься в другом.
Выступающие фигуры имеют параметры базовой плоскости bx и by, а также обычно какой-то параметр, описывающий размер фигуры в основании. Если на изображении представлена только вершина, их значения будут неопределёнными или они перестают быть независимыми. Это может приводить к тому, что аппроксимация начнёт плохо сходиться или закончится ошибкой. Значения параметров надо в этом случае исправить.
Сглаженные гауссовой функцией выступы – конусы и пирамиды – имеют следующие два общих параметра:
- R
радиус кривизны на острие.
- α
Тангенс наклона боковой стороны.
- h
Высота выступа по отношению к горизонтальной базовой плоскости.
- δ
Гладкость, которая определяет ширину грани в форме функции ошибки между нижней и верхней плоскостями.
- L
Период, т.е. то расстояние, после которого форма начинает повторяться.
- p
Покрытие, т.е. часть плоскости, на которой присутствует какая-либо фигура, а не базовая плоскость.
Решетка (простая) содержит только один дополнительный параметр, который задаёт её форму, c. Гребень имеет форму срезанного гиперболического косинуса, где малое значение c соответствует параболическому сечению, в то время, как большое значение c соответствует острому, почти прямоугольному сечению.
Решетка (трёхуровневая) имеет сечение в форме трёх трапециоидов поставленных друг на друга. Соответствующие три параметра высоты h1, h2 и h3 определяют высоту каждого из них. Соответствующие параметры уменьшения толщины q1, q2 и q3 задают насколько толщина верхнего основания соответствующего трапециоида уменьшается по отношению к нижнему (на множитель 1/(1 + qi)). Также нередко полезно взглянуть на производные величины L0, L1, L2 и L3, которые напрямую равны ширинам и производную величину h равную общей высоте.
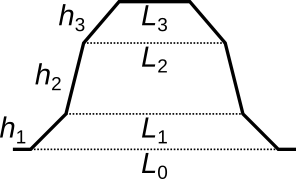
Ширины и высоты трапециоидов, формирующих профиль трёхуровневой решетки. Следует отметить, что ширины это производные параметры, напрямую не аппроксимирующие.
Отверстия имеют параметры s, который задаёт конусность отверстия вследствие наклонных боковых граней, и r, который задаёт кривизну скривления углов. Для обоих параметров нули соответствуют идеальной прямоугольной форме.
Параболическое кольцо является трёхмерной симметричной относительно вращения версией функции аппроксимации Параболическая ступень и управляется в точности теми же самыми параметрами формы.
Сфера имеет только один параметр формы C, задающий кривизну. Радиус доступен в качестве производной величины.
Цилиндр (лежащий) также имеет параметр кривизны C. В дополнение он имеет параметр наклона b∥, задающий наклон базовой плоскости вдоль оси цилиндра.
Гауссиана имеет параметр среднего среднеквадратичного отклонения σmean. Для анизотропных гауссиан он равен геометрическому среднему двух ширин в ортогональных направлениях, доступных в качестве производных величин.
Лоренцева форма имеет параметр полуширины на половине высоты βmean. Для анизотропных лоренцевых функций он равен геометрическому среднему двух ширин в ортогональных направлениях, доступных в качестве производных величин.
Конус имеет параметр R, который определяет радиус конуса у основания.
Пирамида (алмазоподобная) и Пирамида (трёхгранная) имеют параметр L, который определяет длину её стороны (вдоль основания). Поскольку основной ориентацией пирамиды является диагональная, все четыре стороны всё равно будут иметь одинаковую длину даже если параметр анизотропии a не равен единице.
Ступень (двусторонняя) имеет параметр w, который задаёт ширину ступени.