On rencontre parfois des objets ayant des propriétés aléatoires. On admet en général que ces obbjets présentent les propriétés d'auto-affinité sur une certaine plage d'échelles. L'auto-affinité est une généralisation de l'auto-similarité, qui est la propriété essentielle de la plupart des fractales déterministes. Une partie d'un objet auto-affine est similaire à l'objet entier après une mise à l'échelle anisotrope. On considère que de nombreuses surfaces rugueuses appartiennent aux objets aléatoires ayant des propriétés d'auto-affinité, et sont traités comme des fractales. Ces surfaces peuvent bien évidemment être analysées par microscopie à force atomique (AFM). Les résultats de l'analyse fractale de surfaces aléatoires et auto-affines mesurées par AFM sont en général utilisés pour classifier de telles surfaces préparées selon différents procédés technologiques [1,2,3,4].
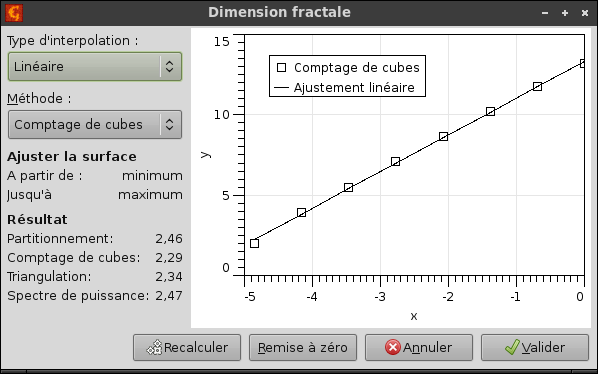
Gwyddion propose différentes méthodes d'analyse fractale, que l'on retrouve dans → → .
- La méthode par comptage de cube [1,2]
- est directement dérivée de la définition de la dimension fractale par comptage de boîte. L'algorithme est basé sur les étapes suivantes : un maillage cubique de constante de maille l est superposé sur la surface selon z. Au départ, l vaut X/2 (où X est la longueur du bord de la surface), ce qui donne un maillage de 2×2×2 = 8 cubes. Puis N(l) est le nombre de tous les cubes contenant au moins un pixel de l'image. La constante de maille l est ensuite réduite par pas de 2 et le procédé se répète jusqu'à ce que l égale la distance entre deux pixels adjacents. La pente du graphe de log(N(l)) par rapport à log(1/l) donne directement la dimension fractale Df.
- La méthode par triangulation [1]
- est très similaire à la méthode par comptage de cube et est elle aussi directement basée sur la dimension fractale par comptage de boîte. La méthode fonctionne de la manière suivante : une grille de dimension unitaire l est placée sur la surface. Celle-ci définit l'emplacement des vertex d'un certain nombre de triangles. Quand, par exemple, l = X/4, la surface est couverte par 32 triangles de différentes aires et inclinés à différents angles par rapport au plan xy. Les aires des triangles sont calculées et sommées pour obtenir une approximation de la surface S(l) correspondant à l. La taille de la grille est ensuite réduite par succesivement par un facteur 2, comme précédemment, et le processus se déroule jusqu'à ce que l correspondeà la distance entre deux pixels adjacents. La pente du graphe de log(S(l)) par rapport à log(1/l) correspond alors à Df − 2.
- La méthode par variance [3,4]
- est basée sur la dépendance d'échelle de la variance du mouvement Brownien fractionnaire. En pratique, dans la méthode par variance on divise la surface en boîtes carrées de taille égale, et la variance (la puissance des valeurs RMS des hauteurs) est calculée pour une taille de boîte particulière. La dimension fractale est calculée à partir de la pente β de la régression linéaire par moindres carrés des points du graphe log-log de la variance, on a alors Df = 3 − β/2.
- La méthode du spectre de puissance [3,4,5]
- est basée sur la dépendance en spectre de puissance du mouvement Brownien fractionnaire. Dans la méthode du spectre de puissance, une tranformée de Fourier est appliquée sur le profil de chaque ligne constituant l'image, permettant d'évaluer le spectre de puissance. Tous les spectres de puissance ainsi calculés sont ensuite moyennés. La dimension fractale est calculée à partir de la pente β de la régression linéaire par moindres carrés des points du graphe log-log du spectre de puissance, on a alors Df = 7/2 + β/2.
Les axes des graphes de dimension fractale affichent des données logarithmiques, les dépendances linéaires mentionnées plus haut correpondent donc ici à des lignes droites. La mesure des axes doit donc être traitée de manière arbitraires.
Notez que les résultats changent en fonction de la méthode utilisée. Ceci vient des erreurs systématiques des approches des différentes analyses fractales.
De plus, les résultats de l'analyse fractale peuvent être fortement influencés par la convolution de la sonde de mesure. Il est donc recommandé de vérifier la carte d'incertitude avant d'appliquer l'analyse fractale. Dans les cas où l'image de la surface est fortement influencée par l'image de la sonde, les résultats de l'analyse fractale peuvent être perturbés de manière importante.
Notez que les algorithmes présents dans le module Analyse Fractale sont aussi utilisés pour le module Correction Fractale et pour l'option Interpolation Fractale de l'outil Supprimer les Points Chauds.
[1] C. Douketis, Z. Wang, T. L. Haslett, M. Moskovits: Fractal character of cold-deposited silver films determined by low-temperature scanning tunneling microscopy. Physical Review B, Volume 51, Number 16, 15 April 1995, 51
[2] W. Zahn, A. Zösch: The dependance of fractal dimension on measuring conditions of scanning probe microscopy. Fresenius J Analen Chem (1999) 365: 168-172
[3] A. Van Put, A. Vertes, D. Wegrzynek, B. Treiger, R. Van Grieken: Quantitative characerization of individual particle sutfaces by fractal analysis of scanning electron microscope images. Fresenius J Analen Chem (1994) 350: 440-447
[4] A. Mannelquist, N. Almquist, S. Fredriksson: Influence of tip geometry on fractal analysis of atomic force microscopy images. Appl. Phys. A 66,1998, 891-895
[5] W. Zahn, A. Zösch: Characterization of thin film surfaces by fractal geometry. Fresenius J Anal Chem (1997) 358: 119-121