En plus des fonction d'analyse des surfaces mesurées, Gwyddion propose plusieurs générateurs de surfaces artificielles pouvant servir pour des tests ou des simulations en dehors de Gwyddion.
Les différents générateurs de surfaces ont un certain nombre de paramètres en commun, ceux-ci permettent de spécifier les dimensions et l'échelle de la surface créée, et de contrôler le générateur de nombres aléatoires. Ces paramètres sont décrits ci-dessous, les paramètres spécifiques à chaque générateur sont décrits dans les sous-sections correspondantes.
Paramètres de l'image :
- Tailles horizontale et verticale
Résolutions horizontale et verticale de la surface générée en pixels.
- Image carrée
Cette option, lorsqu'elle est activée, force les résolutions horizontale et verticale à être identiques.
- Largeur, hauteur
Les dimensions physiques horizontale et verticales de la surface générée. Notez que les pixels sont supposés être carrés, le changement d'une valeur entraîne donc la modification de l'autre.
- Dimension, unité de hauteur
Unités des dimensions latérales (largeur, hauteur) et des valeurs (hauteurs). Les unités choisies ici déterminent aussi les unités des paramètres sans sans dimension des générateurs.
En cliquant sur ce bouton tous les paramètres précédant se retrouvent définis à partir du canal courant.
Notez que si les unités de valeurs sont modifiées, la valeur d'échelle est quant à elle définie par des paramètres spécifiques au générateur, ceux-ci ne sont pas nécessairement déduisibles des propriétés statistiques du canal. Ces paramètres ne sont donc pas recalculés.
- Remplacer le canal courant
Cette option a deux effets. Elle copie d'abord les dimensions et l'échelle du canal courant. Puis elle remplace le canal courant par la surface générée au lieu de créer un nouveau canal.
- Démarrer à partir du canal courant
Cette option a deux effets. Elle copie d'abord les dimensions et l'échelle du canal courant. Puis elle fait démarrer le générateur sur la surface contenue dans le canal courant au lieu de démarrer sur une surface plane. Notez que le résultat ne change pas s'il est dirigé vers le canal courant ou un nouveau canal.
Contôles du générateur aléatoire :
- Graine aléatoire
Il s'agit de la graine du générateur de nombres aléatoires. Le fait de choisir les mêmes paramètres et résolutions ainsi que la même graine aboutira à la génération de la même surface, même sur des ordinateurs différents. Des graines différentes donnent des surfaces différentes ayant des caractéristiques identiques selon les paramètres utilisés par le générateur.
Remplace la graine par un nombre aléatoire.
- Randomiser
Activer cette option permet d'utiliser une nouvelle graine à chaque fois que le générateur est lancé. Cela permet de relancer facilement le générateur avec une nouvelle rgaine en tapant Ctrl-F (voir les raccourcis clavier).
Le module de synthèse spectrale permet de créer des surfaces aléatoires en calculant la transformée de Fourier de la surface à partir des paramètres spécifiés, puis en appliquant la transformée inverse pour obtenir la surface réelle. Les surfaces générées sont périodiques (c'est-à-dire parfaitement juxtaposables).
Les paramètres de Fourier définissent la forme de la PSD, c'est-à-dire les modules des coefficients de Fourier, les phases étant choisies aléatoirement. Actuellement toutes les surfaces générées sont isotropes, c'est-à-dire que leur PSD est radialement symétrique.
- RMS
Moyenne quadratique (RMS, root mean square) des hauteurs (ou des différences au plan moyen, qui est cependant toujours le plan z = 0 ). Le bouton Identique au canal courant ajuste la valeur RMS à celle du canal courant.
- Fréquences minimum et maximum
Fréquences spatiales minimum et maximum. En augmentant la fréquence minimum l'image aura tendance à « s'applatir », c'est-à-dire que les motifs larges seront supprimés. La diminution de la fréquence maximum limitera la finesse des détails.
- Activer le multiplicateur gaussien
Active la multiplication des coefficients de Fourier par une fonction gaussienne, ce qui correspond dans l'espace réel à une convolution par une gaussienne.
- Activer le multiplicateur lorentzien
Active la multiplication des coefficients de Fourier par une fonction proportionnelle à 1/(1 + k2T2)3/4, où T est la longueur d'auto-corrélation. Aussi, le facteur en lui-même n'est pas lorentzien, mais il correspond à une densité spectrale de puissance uni-dimensionnelle lorentizienne, et donnant par ailleurs une fonction d'auto-corrélation exponentielle (voir la section analyse statistique pour une discussion sur les fonctions d'auto-corrélation). Ce facteur décroît relativement lentement, une résolution finie jouera donc un rôle plus important que dans le cas d'une gaussienne.
- Longueur d'auto-corrélation
Longueur d'auto-corrélation du facteur gaussienne ou lorentzien (voir la section analyse statistique pour une discussion sur les fonctions d'auto-corrélation).
- Activer le multiplicateur puissance
Active la multiplication des coefficients de Fourier par un facteur proportionnel à 1/kp, où k est la fréquence spatiale et p est la puissance. Cette option permet de générer différentes surfaces fractales.
- Puissance
Il s'agit de la puissance p.
La méthode de distribution d'objets permet de créer des surfaces aléatoires composées d'éléments de forme spécifique. L'algorithme est simple : les objets spécifiés sont placés aléatoirement sur la surface. Pour chaque objet, les nouvelles hauteurs sont modifiées par max(z, z0 + h), où z est la hauteur de l'objet sur ce pixel (en ayant par hypothèse une base nulle) et z0 et la hauteur minimale courante sur la base de l'objet étant placé. L'algorithme considère que le plan doit être rempli de copies identiques de la surface, celle-ci est donc aussi périodique (c'est-à-dire parfaitement juxtaposable).
- Forme
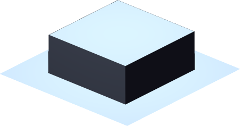
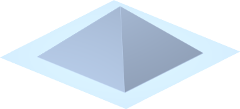
Forme (type) d'objets placés. Les formes suivantes sont actuellement disponibles : demi-sphères, boîtes, pyramides, tétraèdres ainsi que quelques autres plus tordues.
- Couverture
Nombre moyen de fois où un objet couvre un pixel de l'image. Une valeur de 1 indique que la surface serait exactement couverte une fois par les objets, en supposant que ceux-ci la couvrent uniformément sans se superposer. Des valeurs supérieures à 1 impliquent de plus en plus de couches d'objets – ainsi qu'une génération de surface plus lente.
- Taille
Taille latérale des objets, il s'agit en général du carré circonscrit.
- Rapport d'aspect
Rapport des dimensions x et y d'un objet – par rapport aux proportions par défaut.
La modification du rapport d'aspect n'implique pas nécessairement une simple homothétie, par exemple les objets appelés pépites vont passer de demi-sphères à barreaux en fonction du rapport d'aspect.
- Hauteur
Quantité proportionnelle à la hauteur de l'objet, il s'agit en général de la hauteur du plus haut point.
L'option Mettre à l'échelle avec la taille rend la hauteur des objets proportionnelle à leur taille. Sans cette option les hauteurs sont indépendantes des tailles des objets.
Le bouton Identique au canal courant ajuste la hauteur à celle basée sur la valeur RMS du canal courant.
- Type d'objet
Direction selon laquelle la surface est modifiée lors de l'ajout des objets. Les options positif et négatif signifient que les objets formeront respectivement des bosses et des creux. La direction peut aussi être choisie aléatoirement, en choisissant l'option les deux (aléatoire).
- Orientation
Orientation des objets par rapport à l'orientation de base, mesurée dans le sens inverse des aiguilles d'une montre.
- Tronquer
Les formes peuvent être tronquées à une certaine hauteur, ce qui permet de créer des cones ou des pyramides tronquées par exemple. La hauteur de troncature est donnée en proportion de la hauteur totale de l'objet. Une valeur de 1 signifie que la forme n'est pas tronquée, tandis qu'une valeur de 0 supprimerait complètement l'objet.
Chaque paramètre peut être rendu aléatoire pour chacun des objets, à l'aide du paramètre Variance. Concernant les quantités multiplicatives (c'est-à-dire tout excepté l'orientation et la troncature) la distribution est log-normale avec la valeur RMS du logarithme de la quantité donnée par la Variance.
Un bruit alétoire et non-corrélé est généré indépendamment pour chaque pixel. Plusieurs distributions sont disponibles.
- Distribution
Distribution de la valeur du bruit. Celle-ci peut être gausienne, exponentielle, uniforme ou triangulaire.
- Direction
Le bruit peut être symétrique autour de zéro, ou uniquement positif ou négatif. La valeur moyenne de la distribution symétrique est nulle, c'est-à-dire que la valeur moyenne des données ne change pas si l'on y ajoute un bruit symétrique. La valeur moyenne augmente ou diminue si le bruit ajouté est respectivement positif ou négatif.
- RMS
Moyenne quadratique de la distribution de bruit. Plus précisément, il s'agit de la valeur RMS de la distribution symétrique correspondante dans le cas d'une distribution positive ou négative.
Le bruit linéaire correspond au bruit ayant une durée non négligeable donnant typiquement des sauts ou des défauts linéaires dans la direction rapide du scan. Les paramètres Distribution, Direction et RMS ont la même signification que pour le bruit ponctuel. Les autres paramètres contrôlent les caractéristiques latérales du bruit.
Trois types de défauts sont disponibles : les sauts, les rayures et les crêtes. Les sauts représentent des changements de valeur abrupts qui se prolongent jusqu'à la fin du scan (ou jusqu'à ce qu'un autre saut apparaisse). Les rayures représentent des changements locaux de valeur ayant une durée finie, c'est-à-dire que les valeurs retrouvent leur niveau original au bout d'un certain temps. Les crêtes sont similaires mais sur une échlle plus large : elles peuvent s'étendre sur plusieurs lignes.
Les sauts possèdent les paramètres suivants :
- Densité
Nombre moyen de défauts pas ligne de scan, incluant les temps morts (tels que déterminés par le paramètres Dans les lignes).
- Dans les lignes
Fraction du temps pour scanner une ligne correspondant à l'aquisition de données. Le reste du temps correspond au temps mort. Une valeur de 0 signifie que le temps d'aquisition est négligeable devant la durée de scan d'une ligne, et en conséquence les sauts n'apparaissent qu'entre les lignes.
- Cumulatif
Dans le cas des sauts cumulatifs, la valeur aléatoire du saut est toujours ajoutée à la valeur de saut courante ; pour les sauts non cumulatifs la valeur de saut est directement la nouvelle valeur aléatoire.
Les rayures possèdent les paramètres suivants :
- Couverture
Il s'agit de la fraction de l'image couverte par les défauts si ceux-ci ne se recouvrent pas. Comme les défauts peuvent se recouvrir, une valeur de 1 ne signifie pas que toute l'image sera recouverte de défauts.
- Longueur
Longueur des rayure en pixels.
- Variance
Variance de la longueur des rayures, voir le paragraphe Objets pour une description des variances.
Les crêtes possèdent les paramètres suivants :
- Densité
Nombre moyen de défauts par ligne, incluant tous les temps morts (tel que défini par le paramètre dans les lignes).
- Dans les lignes
Fraction de temps pour scanner une ligne correspondant à une acquisition effective des données. Le reste correspond à du temps mort. Une valeur de 1 signifie qu'il n'y a aucun temps mort, c'est-à-dire que des changements de valeur ont lieu en permanence dans l'image. Une valeur de 0 signifie que le temps d'acquisition est négligeable devant la durée de scan d'une ligne, en conséquence les changements de valeur n'ont lieu qu'entre chaque ligne.
- Largeur
Durée moyenne du défaut, mésurée en terme de taille d'image. Une valeur de 1 signifie que la durée moyenne correspondra au temps de scan de toute l'image. Une valeur faible signifie que les défauts n'occuperont principalement qu'une seule ligne.
Les motifs géométriques réguliers font partie des surfaces couramment rencontrées en microscopie en tant que standards ou comme échantillons de test, parmi lesquels on trouve les crénaux, les marches ou les trous. Chaque type de motif a ses propres paramètres géométriques permettant de modifier la forme et les dimensions de différents éléments du motif. Chaque paramètre possède un contrôle de variance similaire à la Synthèse d'objets, qui permet de créer des motifs irréguliers sous certains aspects.
Le placement du motif dans le plan horizontal est contrôlé par les paramètres de l'onglet Placement, commun à tous les types de motif :
- Orientation
Rotation du motif par rapport à une orientation de base, mesurée dans le sens inverse des aiguilles d'une montre.
Cet onglet contient aussi les paramètres de déformation. L'activation de la variation des paramètres géométriques rend la surface plus ou moins irrégulière, mais la forme des éléments reste la même. La déformation est une méthode complémentaire pour introduire une certaine irrégularité en distordant le motif dans le plan xy. Elle possède deux paramètres :
- Amplitude
Amplitude de la déformation latérale. Il s'agit d'une valeur numérique relative déterminant la déformation pouvant être atteinte.
- Echelle latérale
Taille caractéristique des déformations. Elle ne décrit pas à quel point les motifs sont déplacés, mais plutôt à quel point la déformation varie elle-même (rapidement ou lentement) dans le plan horizontal.

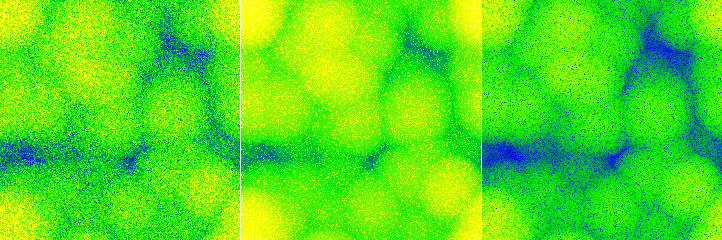
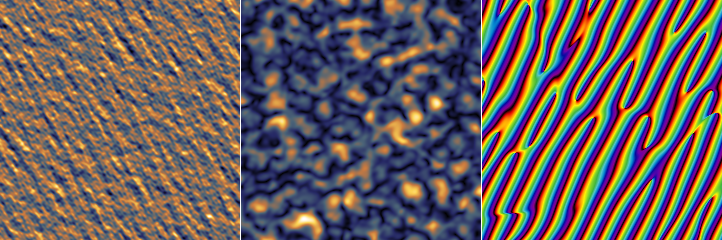
Surfaces artificielles basées sur des motifs : marches raides orientées à 30°, modifiées par une déformation ayant une grande longueur d'autocorrélation (à gauche) ; crénaux séparés de manière non uniforme avec des pentes modérées entre les niveaux haut et bas, ainsi qu'une déformation ayant une courte longueur d'autocorrélation (au centre) ; motif non perturbé de trous arrondis avec une variation importante de taille et profondeur (à droite).
La simulation de croissance colonnaire utilise un algorithme simple de déposition de type Monte Carlo, dans lequel de petites particules tombent sur la surface selon des directions définies par divers paramètres, et s'accrochent à la surface autour du point au niveau duquel elles la rencontrent, augmentant ainsi localement la hauteur. L'effet d'ombrage fait qu'une plus grande partie des particules s'accrochera aux parties les plus élevées de la surface, et qu'une moindre partie atteindra les parties les plus basses. Cette rétroaction positive aboutit à la formation de colonnes. L'algorithme considère le plan horizontal comme étant rempli de copies identiques de la surface, par conséquent la surface générée est elle aussi périodique (c'est-à-dire parfaitement juxtaposable). Le générateur de surface utilise les paramètres suivants :
- Couverture
Nombre moyen de fois où une particule est généré au-dessus de chaque pixel de la surface.
- Hauteur
Augmentation locale de la hauteur lorsqu'une particule s'accroche à un pixel. Comme la taille horizontale de la particule est toujours d'un pixel, la hauteur est elle aussi mesurée en pixels. Une hauteur d'un pixel correspond à des particules cubiques, si l'on considère la croissance de la surface. Du point de vue du calcul de collision, les particules sont considérées comme étant ponctuelles.
- Inclinaison
Angle central d'inclinaison pour lequel les particules sont générées (angle d'incidence). Une valeur de zéro signifie que de très petits angles d'incidence auront la probabilité la plus élevée. Une valeur élevée signifie que les particules rencontreront majoritairement la surface avec une incidence élevée. Toutefois, si la variance de la direction d'incidence (voir ci-après) est élevée, la distribution restera isotrope dans le plan horizontal.
- Direction
Direction centrale d'incidence dans le plan horizontal selon laquelle les particules sont générées. Une variance élevée aboutira à une distribution isotrope dans le plan horizontal, tandis qu'une variance faible donnera une croissance anisotrope.
- Relaxation
Méthode utilisée pour déterminer le pixel sur lequel la particule s'accrochera au final. Il existe deux options pour l'instant. La relaxation faible, avec laquelle seuls les deux derniers pixels immédiatement avant et après la collision sont pris en compte, dans ce cas la particule s'accroche au plus bas des deux. Dans le cas de la relaxation forte, l'algorithme prendra en compte un voisinnage supplémentaire de 3×3 pixels. La particule peut se déplacer vers un pixel plus bas du voisinnage avec une certaine probabilité, avant de s'y accrocher définitivement.
Le dépôt ballistique vertical est l'un des modèles de croissance de film des plus simples. Les particules tombent verticalement sur un site (pixel) choisi aléatoirement. La hauteur du site est incrémentée de la hauteur de la particule. Toutefois, si la nouvelle hauteur s'avère plus faible que celle d'un des quatres sites adjacents, alors la particule collera aux colonnes voisines. La hauteur du site d'impact devient ainsi la hauteur maximale parmi celle des voisins. Il s'agit du seul mécanisme introduisant des corrélations latérales dans la rugosité.
La simulation propose peu de paramètres :
- Couverture
Nombre moyen de fois où une particule est généré au-dessus de chaque pixel.
- Hauteur
Augmentation locale de la hauteur lorsque la particule tombe sur un pixel.
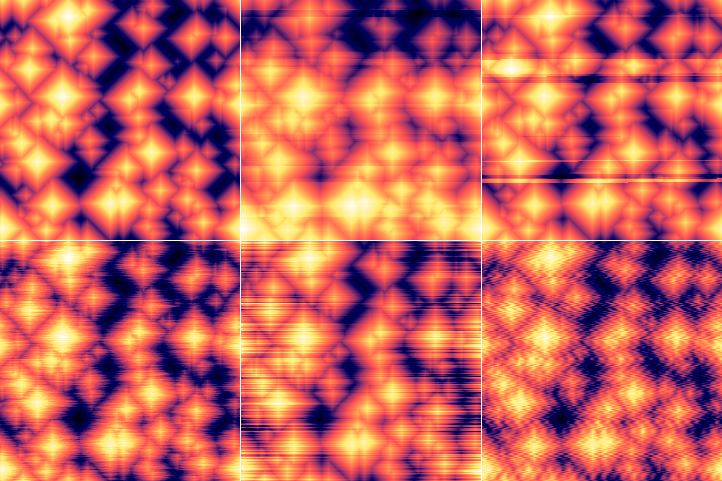
La synthèse par ondes génère une image en utilisant les interférences d'ondes provenant d'un nombre déterminé de sources. En plus de la traditionnelle sinusoïde, quelques autres types d'onde sont disponibles, chacun ayant une forme cosinus et une sinus, l'une et l'autre ne différant que par un déphasage de π/2 dans toutes les composantes fréquentielles. Lorsqu'on considère une onde complexe, la forme cosinus correspond à sa partie réelle, tandis que la forme sinus correspond à sa partie imaginaire.
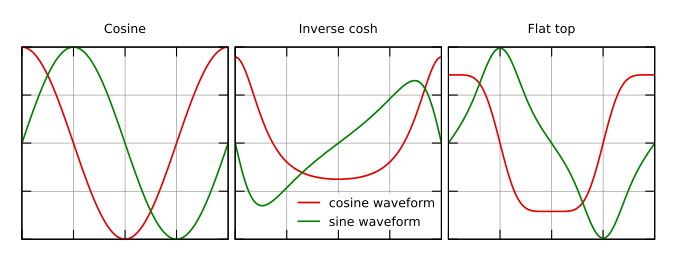
Formes sinus et cosinus des différentes types d'onde disponibles. Seule la forme cosinus est utilisée pour les images de déplacement ; l'onde complexe complète est utilisée pour les images d'intensité et de phase.
Le générateur dispose des options suivantes :
- Quantité
Quantité affichée dans l'image. Le déplacement est la somme des parties réelles. L'amplitude est la valeur absolue de l'onde complexe. La phase correspond à l'angle de phase de l'onde complexe.
- Nombre d'ondes
Nombre de sources ponctuelles à partir desquelles les ondes se propagent.
- Forme d'onde
Forme d'onde décrite plus haut.
- Amplitude
Amplitude approximative (RMS) des hauteurs de l'image générée. Notez qu'elle diffère de l'amplitude des ondes individuelles : dans ce cas l'amplitude des hauteurs croisserait selon la racine carrée du nombre d'ondes, alors que dans les faits elle reste à peu près constante à moins qu'on ne modifie l'amplitude.
- Fréquence
Fréquence spatiale des ondes. Elle est relative à la taille de l'image, c'est-à-dire qu'une valeur de 1.0 correspond à une longueur d'onde égale à la largeur de l'image.
- Centre X, Centre Y
Localisation des sources. La valeur zéro correspond au centre de l'image. Les positions sont aussi mesurées relativement à la taille de l'image. De manière générale, au moins une des valeurs de variance correspondantes devraient être non-nulles ; dans le cas contraire toutes les sources sont au même endroit (on peut tout de même dans ce cas obtenir des motifs intéressants en faisant varier les fréquences).
Ce module implémente un modèle d'Ising hybride hors d'équilibre [1], combinant un modèle d'Ising discret de petite échelle avec un inhibiteur continu et lent.
La variable discrète u a deux valeurs possibles, entre lesquelles elle peut basculer de manière probabiliste selon la loi
où ΔE est le changement d'énergie résultant du basculement et T est la température. L'énergie est donnée par le nombre de voisins dans l'état opposé selon les axes de coordonnées no, le nombre de voisins dans l'état opposé selon les diagonales nd, ainsi que le biais donné par le champ d'inhibition v :
L'inhibiteur continu v est gouverné par une équation différentielle locale couplée à la variable u :
où μ est le couplage d'inhibition et ν est le paramètre de biais. Les conditions aux limites de la simulation sont périodiques, par conséquent les images générées sont elles aussi périodiques (c'est-à-dire parfaitement juxtaposables).
Le calcul dépend des paramètres suivants :
- Nombre d'itérations
Une itération consiste en quatre étapes : une mise à jour par Monte-Carlo de u, une étape temporelle de la solution de l'équation différentielle pour v, une autre étape de Monte-Carlo et enfin une autre étape temporelle de l'équation différentielle. Les valeurs affichées de v correspondent à la seconde mise à jour. La quantité u est la moyenne des deux valeurs entourant dans le temps la valeur correspondante de v. Les images de u sont donc constituées de trois valeurs, et non deux.
- Température T
La température détermine la probablité selon laquelle la variable à deux états u peut basculer vers l'autre valeur s'il en résulte une configuration ayant une énergie supérieure ou équivalente (les basculements abaissant fortement l'énergie ont lieu de manière inconditionnelle). Une température élevée aboutira à une séparation moindre entre les deux domaines u .
- Force de l'inhibiteur B
Force avec laquelle la variable continue biaise l'énergie de chaque pixel. Une valeur élevée donnera une à l'inhibiteur une influence plus élevée comparée à celle de la tension de surface.
- Couplage de l'inhibiteur μ
Facteur de couplage entre u et v dans l'équation différentielle pour v.
- Biais ν
Biais dans l'équation différentielle pour v vers des valeurs plus faibles ou plus élevées.
- Étape temporelle de Monte-Carlo
Étape temporelle correspondant à une étape de Monte-Carlo dans l'équation différentielle. Ce paramètre détermine donc la vitesse relative des deux processus.
- Hauteur
Plage de valeur des images créées par le module.
Cette simulation propose un modèle d'agrégation limitée par diffusion basé sur une méthode de Monte-Carlo discrète. Des particules en forme de pixel tombent sur la surface et se déplacent sur celle-ci jusqu'à ce qu'elles adhèrent à un agrégat, formant ainsi lentement une mono-couche. Le flux de particules est faible de manière à ce que quelques particules seulement soient libres de se déplacer à un moment donné ; celles-ci peuvent donc parcourir un chemin conséquent avant d'adhérer à la surface. L'utilisation des paramètres par défaut aboutit à la formation d'agrégats en forme de « flocons fractals ».
Le calcul utilise les paramètres suivants :
- Couverture
Nombre moyen de fois où une particule tombe sur un pixel donné. Une valeur de couverture de 1 signifie que la surface serait couverte par une mono-couche, en supposant que les particules la couvre uniformément.
- Flux
Nombre moyen de fois où une particule tombe sur un pixel donné à chaque étape de la simulation. Un flux faible aboutit à des structures plus étendues car les particules diffusent pendant une durée plus longue avant de rencontrer une autre particule. La valeur est donnée en logarithme décimal, indiqué par l'unité log₁₀.
- Hauteur
Hauteur d'une particule, ce qui donne la hauteur des sauts dans l'image finale.
- Probabilité d'adhérence
Probabilité qu'une particule libre adhérera et cessera donc de se déplacer lors du contact avec une autre particule. La probabilité que la particule adhère si elle touche deux ou trois particules augmente en fonction de cette valeur. La probabilité d'adhérence est toujours nulle pour une particule isolée, et vaut toujours un si la particule est entourée de quatre particules voisines.
- Probabilité d'activation
Probabilité qu'une particule n'ayant pas adhéré se déplace si elle touche une autre particule. La probabilité de toucher plus de particules décroît selon une loi en puissance de la probabilité pour une particule unique. Les particules sans aucune voisine peuvent toujours se déplacer librement.
- Probabilité de la barrière de Schwoebel
Une particule tombant sur le dessus d'un amas déjà formé a une probabilité réduite de descendre sur la couche précédente à cause de ce que l'on appelle la barrière de Schwoebel. Si ce paramètre vaut 1 cette barrière est inexistante, c'est-à-dire que les particules sont libres de descendre sur la couche précédente. À l'inverse, une probabilité nulle signifie que les particules ne peuvent jamais descendre sur la couches précédente. A particle that has fallen on the top of an already formed cluster can have reduced probability to descend to the lower layer due to so called Schwoebel barrier. If this parameter is 1 there is no such barrier, i.e. particles can descend freely. Conversely, probability 0 means particles can never descend to the lower layer. La valeur est donnée en logarithme décimal, indiqué par l'unité log₁₀.
Notez que certaines combinaisons de paramètres, par exemple un très faible flux combiné à une très faible probabilité de la barrière de Schwoebel, peuvent aboutir à des temps de calcul extrêmement longs.
Le module de synthèse de maillage crée des surfaces basée sur des mailles bi-dimensionnelles aléatoires. Il comporte deux parties principales. La première, contrôlée par l'onglet Maillage, permet la création d'un ensemble de points dans le plan organisés selone un maillage plus ou moins aléatoire. La seconde, contrôlée par l'onglet Surface, permet la construction de la surface basée sur des quantités calculées par pavage de Voronoi et/ou par triangulation de Delaunay sur l'ensemble des points définis précédemment.
La création du maillage est contrôlée par les paramètres suivants :
- Maillage
Type de maille de base. La maillage aléatoire consiste en des points placés aléatoirement. Les autres types (carrée, hexagonale, triangulaire) correspondent à des arrangements de points réguliers.
- Taille
Taille moyenne des cellules. Ce paramètre décrit la densité moyenne despoints. Elle est égale au côté du carré si le même nombre de points était organiséé en un maillage carré.
- Relaxation du maillage
Quantité de relaxation permise pour la maille. Le processus de relaxation éloigne les points de leurs proches voisins et les rapproche des espaces vides. Le résultat final est que la taille de cellule devient de plus en plus uniforme. Évidemment, la relaxation n'a aucun impact sur un maillage régulier. Notez que la relaxation nécessite un repavage progressif et qu'une valeur élevée de relaxation peut sensiblement ralentir la génération de la surface.
- Relaxation des hauteurs
Quantité de relaxation permise pour les valeurs aléatoires assignées à chaque point (voir plus bas). Le processus de relaxation est similaire à la diffusion et aboutit à un lissage des valeurs aléatoires.
- Orientation
Rotation du maillage par rapport à l'orientation de base, mesurée dans le sens inverse des aiguilles d'une montre. Elle n'est disponible que pour les maillages réguliers car le maillage aléatoire est isotrope.
- Amplitude, Échelle latérale
Paramètres contrôlant la déformation du maillage. Ils ont la même signification que dans la synthèse de motifs.
La surface finale est construite selon une somme pondérée d'un ensemble de quantités basiques dérivées du pavage de Voronoi ou de la triangulation de Delaunay. Chaque quantité peut être activée ou non. Lorsque l'une d'elles est sélectionnée dans la liste, sa pondération et ses paramètres de seuil peuvent être modifiés grâce aux curseurs. Les seuils hat et bas permettent de couper la plage de valeurs (qui est toujours normalisée à [0, 1]) en substituant toutes les valeurs supérieures au seuil haut par la valeur de seuil et en faisant l'inverse pour le seuil bas.
Certaines quantités sont calculées uniquement d'après les coordonnées latérales. D'autres sont calculées à partir de valeurs aléatoires (« heuteurs ») appliquées à chaque point de l'ensemble. On trouve parmi les quantités proposées :
- Aléatoire constant
Interpolation arrondie entre les valeurs aléatoires assignées à chaque point de l'ensemble. Cela signifie que chaque cellule de Voronoi est remplie par une valeur alétoire constante.
- Aléatoire linéaire
Interpolation linéaire entre les valeurs aléatoires assignées à chaque point de l'ensemble. La surface est alors continue, chaque triangle de Delaunay étant une facette.
- Aléatoire bosselé
Interpolation similaire à la précédente, mais cette fois non linéaire, aboutissant à des zones relativement planes autour de chaque point.
- Distance radiale
Distance au point le plus proche.
- Distance segmentée
Distance au bord le plus proche de la cellule de Voronoi, mise à l'échelle pour chaque segment de la cellule de manière à ce que le point soit à la même distance de tous les bords de sa cellule.
- Aléatoire segmenté
Quantité identique à la distance segmentée, mais multipliée par la valeur aléatoire assignée au point.
- Distance de bord
Distance au bord le plus proche de la cellule de Voronoi.
- Bord aléatoire
Quantité identique à la distance de bord, mais multipliée par la valeur aléatoire assignée au point.
- Second point le plus proche
Distance au second point le plus proche de l'ensemble.
Ce module génère des surfaces dont les profils sont similaires à des échantillons de mouvement brownien fractionnaire. La méthode de construction n'est cependant pas très sophistiquée. On démarre des coins de l'image, puis les points intérieurs sont interpolés linéairement de manière récursive le long des axes vertical et horizontal, en y ajoutant du bruit dont l'échelle est liée à la distance via l'exposant de Hurst. Certaines surfaces générées seront très similaires à celles obtenues avec la synthèse spectrale, mais le fait de les construire dans l'espace direct plutôt que dans l'espace des fréquences permet des modifications différentes de leurs propriétés.
Le générateur propose les paramètres suivants :
- Exposant de Hurst
Valeur nominale de l'exposant de Hurst H. Pour les valeurs normales entre 0 et 1, la racine carrée de la fonction de corrélation hauteur-hauteur augmente selon la H-ème puissance de la distance. L'algorithme de construction permet aussi les valeurs négatives car il s'arrête à la résolution finie d'un pixel.
- Échelle de stationnarité
Échelle à laquelle la stationnarité est imposée (notez que le mouvement brownien fractionnaire n'est pas stationnaire). Elle a peu d'effet lorsque qu'ell est comparable ou plus largue que la taille de l'image. Par contre lorsqu'elle est petite l'image se retrouve « homogénéisée » au lieu d'être auto-similaire au-delà de cette échelle.
- Distribution
Distribution du bruit ajouté lors de la génération. Les distributions uniforme et gaussienne donneront globalement les mêmes surfaces (d'un point de vue statistique) ; le second type est toutefois plus rapide. Des distributions à « queue lourde », c'est-à-dire exponentielle ou plus particulièrement en puissance, aboutiront à des pics et des vallées plus prononcés.
- Puissance
Puissance α pour la distribution du même nom. La densité de probabilité est proportionnelle à
- RMS
Moyenne quadratique des hauteurs (ou de la différence par rapport au plan moyen, qui est toutefois toujours le plan z = 0). Notez que cette valeur s'applique à l'image générée, et non au procédé qui la génère, qui n'a lui pas de valeur RMS finie. Le bouton identique au canal courant ajuste la valeur RMS à celle du canal actif lors du lancement du module.
Ce module transforme les valeurs de manière à forcer certaines propriétés statistiques. La distribution des valeurs peut être forcée à devenir gaussienne, tout en conservant la valeur moyenne et le rugosité RMS, ou uniforme, les valeurs minimale et maximale étant cette fois préservées. Il est aussi possible de forcer la distribution de manière à ce qu'elle soit identique à celle d'un autre champ de données, que l'on pourra sélectionner dans la partie gabarit.
La transformation conserve l'ordonnancement des valeurs, c'est-à-dire que si un point est plus élevé qu'un autre avant la transformation, alors il restera plus élevé après cette transformation. L'option traitement des données permet d'appliquer la transformation à l'ensemble de l'image (image entière) ou à chaque ligne séparément, avec la même distribution (par ligne (identique)). Notez que dans ce dernier cas, si une image gabarit est utilisée, chaque ligne de l'image transformée aura approximativement la même distribution que celle du gabarit.
Un autre type de transformation peut être appliqué, il s'agit de la discrétisation des valeurs en un nombre donné de niveaux. Cette opération est possible en sélectionnant l'option niveaux discrets. Deux types de discrétisations sont possibles, soit les niveaux de hauteur sont équidistants entre les valeurs minimale et maximale (unifome), soit ils sont calculés de manière à ce qu'après la transformation chaque niveau ait approximativement le même nombre de pixels (surface identique).