Gwyddion propose plusieurs fonctions basiques pour la visualisation de données volumiques et l'extraction de données de dimensions inférieurs (coupes, courbes). Quelques fonctions spécialisés, orientées vers le traitement de données volumiques sous forme de courbes (ou spectres) pour chaque pixel, sont aussi disponibles. Celles-ci sont toutes présentes dans le menu de la fenêtre principale.
Gwyddion interprète la plupart du temps les données volumiques comme un ensemble de courbes, chacune étant rattachée à un pixel dans le plan xy, ou de manière alternative comme un empilement d'images selon l'axe z. Cela signifie que les fonctions attribuées aux données volumiques traiteront en particulier l'axe z. Si vous comptez importer dans Gwyddion des données volumiques comportant deux dimensions spatiales et une dimension pariculière, assurez-vous que l'axe particulier corresponde à z.
Les opérations élémentaires sur les données volumiques sont les suivantes :
Change les dimensions physiques, les unités ou les échelles ainsi les décalages latéraux. Cela peut s'avérer utile pour corriger les données brutes importées avec de mauvaises échelles ou pour une simple recalibration des dimensions et des valeurs.
Cette fonction inverse le signe de toutes les valeurs des données volumiques.
Lorsque l'axe z ne correspont pas à une dimension spatial, son échantillonnage peut être irrégulier, contrairement aux axes d'imagerie x et y qui eux seront toujours réguliers. Cet aspect est réprésenté dans Gwyddion en associant des données uni-dimensionnelles avec l'axe z, appelées calibration selon Z.
Cette fonction permet d'afficher la calibration selon Z, de la supprimer, de l'extraire sous forme de graphe ou d'attacher une nouvelle calibration à partir d'un fichier texte. Dans ce dernier cas, chaque ligne du fichier doit contenir une valeur la véritable valeur de l'axe z pour le plan correpondant ; bien évidemment, le nombre de lignes doit correspondre au nombre de plans images présent dans les données volumiques.
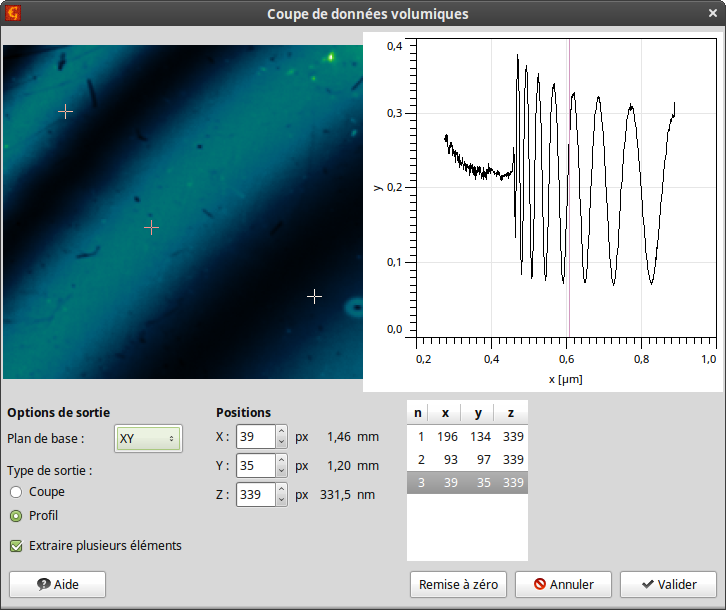
On peut extraire des profils selon n'importe que axe ainsi que des coupes selon un plan orthogonal à n'importe quel axe avec la fonction → .
La coupe dans le plan sélectionné, appelé plan de base, est toujours affichée dans la partie gauche, la coupe selon l'axe orthogonal restant est quant à lui affiché dans la partie droite de la fenêtre. Vous pouvez modifier le point à partir duquel le profil est extrait en déplaçant le point sélectionné dans l'image. De manière similaire, la localisation du plan de coupe peut être modifiée en sélectionnant un point sur le graphe du profil. Les deux valeurs peuvent aussi être entrée manuellement selon X, Y et Z (en pixels).
Vous pouvez choisir entre l'extraction de coupe ou de profil en sélectionnant le type de sortie. Cela n'aura pour seule conséquence que la création de l'image à gauche ou le profil à droite lorsque vous appuierez sur .
Il est aussi possible de prendre plusieurs profils ou coupes en une seule fois. Si la case extraire plusieurs éléments est activée, une liste des points sélectionnés apparaîtra sur la droite. Dans ce cas le type de sortie a une influence sur la sélection. Dans le mode coupe vous ne pourrez sélectionner qu'un seul point dans l'image (qui déterminera le profil affiché sur le graphe), mais vous pourrez sélectionner plusieurs points sur le graphe, chacun déterminant un plan de coupe. À l'inverse, le mode profil vous ne pourrez sélectionner qu'un seul point sur le graphe (déterminant le plan image affiché) mais vous pourrez sélectionner plusieurs points sur l'image, déterminant ainsi la localisation des profils.
Le basculement d'un type de sortie à un autre lorsque cette option est activée aura pour conséquence de réduire l'ensemble de coordonnées sélectionnées à un seul point. Vous pouvez aussi utiliser le bouton pour réduire la sélection à un seul point si vous souhaitez complètement redéfinir la sélection.
On peut réaliser une caractérisation basique des profils le long de l'axe z à l'aide de la fonction → . Cette fonction crée une image formée par les caractéristiques statistiques des profils pris selon l'axe z. L'ensemble des quantités statistiques disponibles est identique à celui de l'outil statistiques de lignes/colonnes.
La sélection duale image/graphe fonctionne de manière similaire à l'extraction de coupes et de profils. La principale différence réside dans le fait qu'un intervalle peut être sélectionné dans le graphe, définissant la partie de l'empilement d'images à partir de laquelle la statistique sera calculée. L'intervalle peut aussi être entré manuellement dans la partie plage. L'image sur la gauche affiche les caractéristiques calculées et correspond à ce que sortira le module. En sélectionnant un autre point dans l'image, vous modifierez le profil affiché sur le graphe, ce qui peut être utile pour déterminer la bonne plage à sélectionner. Toutefois, cela n'aura aucune influence sur la sortie.
Les techniques d'imagerie spectroscopique telles que la force-distance (F-D) pour les applications en cartographie nano-mécanique quantitative (QNM, Quantitative Nanomechanical Mapping), la relation courant-tension (I-V) dans le domaine des semi-conducteurs, ou la fluorescence Raman pour la caractérisation des matériaux, nécessitent de mesurer un spectre en chaque point mesuré de l'échantillon. Travailler avec de telles données n'est pas chose aisée, car il faut traiter des milliers de spectres et analyser chacun d'eux. Si l'échantillon contient un nombre limité de régions ayant chacune des spectres similaires, alors certaines techniques permettant de grouper ces spectres peuvent être particulièrement utiles. Une de ces techniques consiste réaliser une analyse par partitionnement. Gwyddion propose actuellement deux méthodes : les K-moyennes et les K-médianes.
Les deux algorithmes tentent de trouver K partitions, les spectres étant similaires dans chacun d'eux, en maximisant les différences entre partitions. Le paramètres nombre de partitions correspond donc au nombre K de partitions que vous souhaitez obtenir au final. Les décimales de convergence et le nombre d'itérations max. gèrent les critères de convergence des algorithmes, qui s'arrêteront si la précision requise est atteinte pour la position des centres des partitions ou si le nombre de cycle de convergence dépasse la limite autorisée. Une précision plus importante nécessitera un nombre plus élevé de cycles, la seconde limite est généralement utilisée pour éviter les optimisations interminables lorsque la précision demandée est trop importante pour les données utilisées.
Le paramètre normaliser correspond à une technique plutôt expérimentale donnant des résultats intéressants pour l'imagerie spectroscopique. Si les intensités des spectres ne vous intéressent pas et que vous souhaitez partitionner les données par similarité des fréquences moyennes des spectres (ce qui est typiquement le cas dans le domaine de la microscopie Raman), alors cochez cette case. L'arrière-plan basse fréquence sera alors soustrait en prenant en compte le minimum dans la fenêtre glissante, puis normalise le spectre de manière à ce que l'intensité moyenne soit égale à 1. Les deux modules génèrent deux types de données : l'un indique à quelle partition appartient le spectre courant, l'autre affiche l'erreur — la différence entre le spectre courant et le centre de la partition associée. Si la normalisation est activée, alors un troisième type de donnée affiche la valeur par laquelle l'intensité spectrale a été divisée lors de la normalisation (après filtrage basse fréquence). Par ailleurs, un graphe des spectres correspondant aux centres des partitions est extrait.
Les algorithmes utilisés dans ces deux modules sont basés sur le partitionnement par apprentissage non supervisé : respectivement les K-moyennes et les K-médianes. Nous considérons chaque spectre (graphe le long de l'axe z) comme étant un point dans l'espace multi-dimensionnel avec un nombre de dimensions égal au nombre de points dans le graphe. Nous définissons la distance entre les points comme la racine carrée de la somme des différences au carré le long de chaque direction (norme L2). Puis nous initialisons les deux algorithmes en choisissant K points aléatoirement dans le volume en tant que centres des partitions. Puis on applique l'algorithme habituel à deux étapes : on assigne chaque point à la partition la plus proche puis on déplace le centre des partitions. La différence entre les modules réside dans la manière dont est calculé le centre des partitions : il s'agit de la valeur moyenne des points des partitions dans le cas des K-moyennes, et de la médiane le long de chaque direction dans le cas des K-médianes. Les résultats de la dernière itérations sont renvoyées vers le programme pour affichage.
Pour les K-moyennes, l'option supprimer les points aberrants modifie l'algorithme de calcul du centre des partitions en n'incluant que les points sous le seuil des points aberrants multiplié par la varition σ des données de chaque partition. Il enlève les points aberrants individuels (tels que les pics ou les impacts de rayons cosmiques en spectroscopie Raman) du calcul, rendant les centres des partitions plus propres et distincts, et décale aussi les bords entre partitions proches vers des centres de densité de points maximale moins perturbés par des points aberrants trop éloignés.