Двумерное преобразование Фурье доступно в меню → → , где реализовано быстрое преобразование Фурье (БПФ, FFT). Преобразование Фурье раскладывает сигнал на его гармонические составляющие, и, таким образом, его можно использовать при изучении спектральных частот, присутствующих в данных СЗМ.
Модуль 2D БПФ предлагает несколько вариантов вывода данных:
- Модуль — абсолютное значение комплексного коэффициента Фурье, пропорциональное квадратному корню функции спектральной плотности мощности (ФСПМ).
- Фаза — фаза комплексного коэффициента (используется редко).
- Действительное — действительная часть комплексного коэффициента.
- Мнимое — мнимая часть комплексного коэффициента.
и некоторые их сочетания для удобства.
Радиальные сечения двумерной ФСПМ можно удобно получить с помощью операции 2D PSDF. Несколько других функций, рассчитывающих спектральные плотности описаны в разделе Статистический анализ. Также возможно фильтровать изображения в частотном представлении (Фурье-пространстве) используя одномерный или двумерный фильтры на основе быстрого преобразования Фурье (БПФ) или простое разделение частот.
Для не зависящего от масштаба и поворота сравнения текстур может оказаться полезным преобразовать ФСПМ из декартовых координат частот в координаты, состоящие из логарифма пространственной частоты и её направления. Масштабирование и поворот в новых координатах становятся простыми смещениями. Функция → → непосредственно расчитывает преобразованную ФСПМ. Безразмерная горизонтальная координата это угол (от 0 до 2π), вертикальная это логарифм частоты. Также возможно сгладить ФСПМ гауссовым фильтром заданной ширины перед преобразованием.
Следует отметить, что преобразование Фурье считает данные бесконечно протяженными, и, следовательно, накладывает некоторые периодические граничные условия. Поскольку реальные данные не обладают этими свойствами, необходимо использовать некоторую оконную функцию для подавления данных на границах изображения. Если вы этого не сделаете, БПФ будет считать данные обработанными прямоугольной функцией окна, которая имеет действительно скверный Фурье-образ, что приводит к искажению Фурье-спектра.
Gwyddion предлагает на выбор несколько функций окна. Большинство из них образовано набором синусов и косинусов, которые корректно приглушают данные на краях. В следующей таблице формул для функций окна независимая переменная x лежит в диапазоне [0, 1], что соответствует нормализации абсциссы; для простоты переменная ξ = 2πx используется в ряде формул. Доступные виды оконных функций включают в себя:
| Название | Формула |
|---|---|
| Нет | 1 |
| Прямоугольное | 0.5 в граничных точках, 1 во всех остальных |
| Ханн | |
| Хэмминг | |
| Блэкмен | |
| Ланцош | |
| Велч | |
| Наттолл | |
| Плоская вершина | |
| Кайзер α | , где I0 — модифицированная функция Бесселя нулевого порядка и α — параметр. |
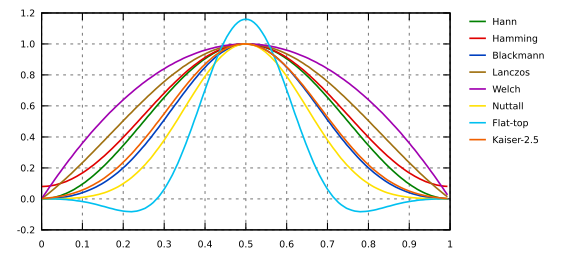
Оконные функции: Ханна, Хэмминга, Блэкмена, Ланцоша, Велча, Наттола, с плоской вершиной, Кайзера 2,5.
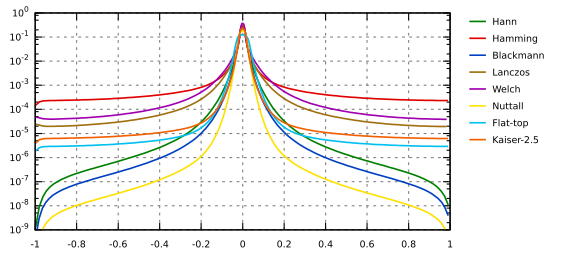
Огибающие частотного отклика оконных функций: Ханна, Хэмминга, Блэкмена, Ланцоша, Велча, Наттола, с плоской вершиной, Кайзера 2,5.
→ →
Одним из наиболее удачных способов удаления шума на определённых частотах из изображения является Фурье-фильтрация. Сначала вычисляется прямое преобразование Фурье изображения. Затем к результату преобразования применяется фильтр. После этого обратное преобразование используется для получения отфильтрованного изображения. Gwyddion использует быстрое преобразование Фурье (БПФ или FFT) для существенного ускорения этого большого расчёта.
При использовании одномерного фильтра БПФ частоты, которые должны быть удалены со спектра (тип подавления: убрать) или подавлены до значения соседних частот (тип подавления: выровнять), могут быть выбраны отметкой нужных областей на графике спектра мощности. Выбранная область может быть легко инвертирована использованием опции "тип фильтра". Одномерная фильтрация БПФ может использоваться как для горизонтального, так и для вертикального направления.
→ →
Двумерная фильтрация БПФ работает подобно одномерному варианту (см. выше), но использует двумерное преобразование Фурье. Следовательно, пространственные частоты, которые нужно отфильтровать должны быть выбраны в двумерном пространстве с использованием редактора маски. Поскольку частоты измеряются относительно центра изображения (который соответствует нулевой частоте), маску можно прикрепить к центру (началу координат) в процессе редактирования. Также доступны различные режимы отображения и вывода результата, которые не требуют разъяснений – модуль может выводить изображение или коэффициенты БПФ (или оба).
→ →
Простой альтернативой двумерной фильтрации с помощью БПФ будет разделение изображение на составляющие с низкими и высокими пространственными частотами используя простые фильтры нижних и верхних частот. В зависимости от выбранной опции тип вывода модуль разделения частот может создавать либо низкочастотное, либо высокочастотное изображение, либо оба
Порог задаёт пространственную частоту, которая показывается как относительная доля частоты Найквиста и также как соответствующая пространственная длина волны. Если Ширина пороговой функции задаётся нулевой, фильтр будет иметь узкий порог частоты. Для ненулевых значений переход будет иметь форму функции ошибки erf с заданной шириной.
Фильтрация в частотной области может приводить к артефактам вдоль границ изображения. Вследствие этого модуль предлагает несколько вариантов работы с граничной областью помимо варианта Нет, который годится только для периодических данных (или другим способом непрерывных при переходе через границу изображения). По Лапласу и Зеркально расширяют изображение решением уравнения Лапласа или зеркальным отображением, соответственно, точно таким же способом, как и функция Расширить. Гладкий переход применяет к строкам и колонкам изображения одномерный гладкий метод расширения, который используется в инструменте измерения шероховатости для подавления артефактов на границе.