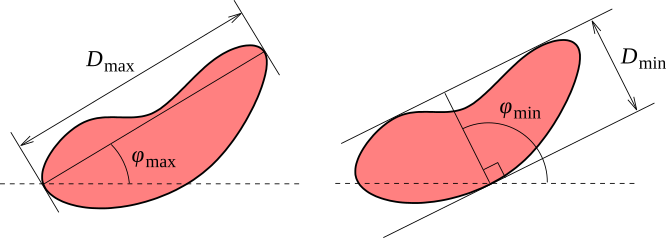
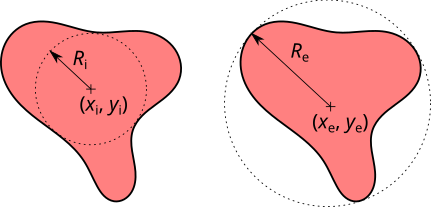
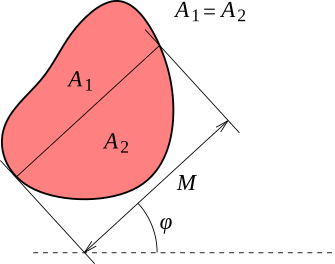
В Gwyddion реализовано несколько алгоритмов для работы с зёрнами. Прежде всего, можно использовать простые пороговые алгоритмы (порог по высоте, наклону и кривизне). Эти процедуры могут быть очень эффективны для анализа частиц (чтобы пометить частицы лежащие на ровной поверхности).
→ →
Выделение по порогу это основной метод выделения зёрен. В этом модуле реализованы пороги по высоте, наклону и кривизне. Результаты отдельных пороговых методов можно объединять вместе используя логические операторы.
→ →
Автоматический метод Оцу выделения зёрен по порогу классифицирует значения данных в два класса, минимизируя дисперсию внутри класса для обоих. Метод хорошо подходит для изображений, которые содержат два относительно хорошо определённых диапазона значений.
→ →
Другой вариант функции выделения зёрен основан на обнаружении краёв (локальной кривизне функции высоты). Изображение обрабатывается фильтром «разница гауссианов\quote> »
→ →
Зёрна, которые касаются границ изображения, можно удалить используя эту функцию. Это может быть полезно в том случае, когда эти зёрна нужно рассматривать как неполные и их нужно исключить из анализа. Некоторые другие функции, которые можно использовать для модификации формы зерён после их выделения, вызываются из инструмента Редактор маски.
→ →
Для более сложных структур данных эффективность пороговых алгоритмов может оказаться весьма плохой. Для этих данных выделение зёрен или частиц более эффективно можно проводить с помощью алгоритма водораздела.
Алгоритм водораздела обычно задействуется для определения локальных минимумов и разделения изображения на сегменты в обработке изображений. Поскольку проблема определения положения зёрен может сводиться к проблеме нахождения локальных экстремумов на поверхности, этот алгоритм также можно использовать для нужд разделения и выделения зёрен. Для удобства в дальнейшем мы будем считать данные инвертированными в направлении z при описании этого алгоритма (т.е. вершины зёрен формируют локальные минимумы в нижеследующем тексте). Мы применяем две стадии анализа зёрен (см. [1]):
- Фаза обнаружения зёрен: В каждой точке инвертированной поверхности помещается виртуальная капля воды (количество воды регулируется параметром Размер капли). В случае, если капля не находится в локальном минимуме, она следует по пути наискорейшего спуска чтобы минимизировать свою потенциальную энергию. Как только капля достигает любого локального минимума, она остаётся там и покоится на поверхности. Подобным образом она частично заполняет объём локального минимума (см. рисунок ниже и его подпись). Этот процесс повторяется несколько раз (параметр Число шагов). В результате получается система водоёмов различного размера, заполняющих впадины в инвертированной поверхности. После этого рассчитывается площадь каждого водоёма и наименьшие из них отбрасываются в предположении, что они формируются в локальных минимумах, образованных шумом (все водоёмы размером меньше, чем задано параметром Порог, удаляются). Большие водоёмы используются для определения положения зёрен для разделения на следующем шаге. Подобным образом можно устранить шум на данных АСМ.
- Фаза разделения: Зёрна, найденные на первом шаге, помечаются (каждое своим уникальным номером). Капли воды продолжают падать на поверхность и заполнять локальные минимумы (количество воды регулируется параметром Размер капли). Общее число шагов падения капли в каждую точку поверхности регулируется параметром Число шагов. Поскольку зёрна уже обнаружены и помечены после первого шага, следующие пять ситуаций возможны после достижения каплей локального минимума.
- Капля достигла места, ранее отмеченного как определённое зерно. В этом случае капля объединяется с зерном, т.е. помечается как часть того же зерна.
- Капля достигла места, где нет зерна, но отмеченное зерно найдено в ближайшей окрестности капли. В этом случае капля снова объединяется с зерном.
- Капля достигла места, где нет зёрен, и при этом зёрен не было даже в ближайшей окрестности капли. В этом случае капля никак не помечается.
- Капля достигла места, где нет зерна, но более одного отмеченного зерна найдено в ближайшей окрестности. (т.е. в окрестности нашлось два разных зерна). В этом случае капля помечается как граница зерна.
- Капля достигла места, помеченного как граница зерна. В этом случае капля также помечается как граница зерна.
Таким путём мы определяем положения отдельных зёрен и затем определяем объём, занятый каждым зерном по отдельности. Если нас интересуют на поверхности не зёрна (выпуклости), а долины (впадины), можно использовать параметр Инвертировать высоту.
→ →
Эта функция реализует другой подход, основанный на алгоритме водораздела, в данном случае классический алгоритм Винсента для водораздела в цифровых пространствах [2], который применяется к предобработанному изображению. В общем случае результатом будет изображение, полностью сегментированное на фрагменты, каждый пиксель либо принадлежит фрагменту, либо разделяет два соседних. По умолчанию алгоритм помечает впадины. Чтобы пометить направленные вверх зёрна, что встечается чаще на изображениях АСМ, можно использовать опцию Инвертировать высоту.
Для предобработки доступны следующие параметры:
- Гауссово сглаживание
Дисперсия гауссова сглаживающего фильтра, применяемого к изображению. Нулевое значение соответствует отсутствию сглаживания.
- Добавить градиент
Относительный вес локального градиента, добавленного к данным. Большие значения соответствуют тому, что области с большими локальными уклонами будут стремиться стать границами зёрен.
- Добавить кривизну
Относительный вес локальной кривизны, добавленной к данным. Большие значения соответствуют тому, что локальные вогнутые области будут стремиться стать границами зёрен.
- Высота барьера
Относительный уровень высоты, выше которого пиксели никогда не присваиваются к любому из зёрен. Если не выставлено в 100%, эта настройка создаёт исключение для свойства полной сегментации.
- Уровень предзаполнения
Относительный уровень высоты, до которого поверхность предзаполняется, затирая любые детали на дне глубоких впадин.
- Предварительно заполнять с минимумов
Относительный уровень высоты, до которого поверхность предзаполняется из каждого локального минимума, затирая любые детали на дне впадин.
→ →
Для того, чтобы перенести сегментацию с одного изображения на другое похожее, или с более мелкого фрагмента на полное большое изображение можно использовать модуль логистической регрессии. У модуля есть два режима работы, в режиме обучения ему нужна маска зёрен, которая должна присутствовать на изображении, и он обучает логистическую регрессию для этой маски. После обучения можно использовать этот модуль для выделения зёрен на новых изображениях. В обоих режимах работы модуль создаёт вектор признаков для каждой точки из точек текущего изображения, применяя к нему набор различных фильтров. На данный момент доступны следующие признаки:
- Гауссово размытие
Гауссовы фильтры с длиной в 2, 4, 8 и т.д. пикселей. Число гауссовых фильтров может быть выбрано с помощью опции Число гауссиан.
- Производные Собеля
Фильтры первых производных Собеля для направлений X и Y.
- Лапласиан
Оператор Лапласа (суммы вторых производных).
- Гессиан
три элемента матрицы вторых производных Гесса, по одной, реализующей двойное дифференцирование по направлениям X и Y и один со смешанной производной (поскольку диагональные элементы должны быть равны в данном случае).
Все фильтры производных если их выбрать применяются как к оригинальному изображению, так и к каждому из уровней сглаживания гауссовыми фильтрами, если они включены. Каждый из слоёв признаков считается с помощью оператора свёртки и после этого нормализуется.
Параметр регуляризации позволяет регуляризовать логистическую регрессию, большее значение означает, что параметры регрессии более ограничены и не могут принимать очень большие значения.
Следует отметить, что для начала обучения необходима маска интересующих особенностей (зёрен) на исходном изображении, или в результате обучения получится нулевой результат. Фаза обучения может быть очень медленной и требовательной к памяти, особенно для больших изображений и большого числа признаков. Результаты обучения сохраняются между вызовами функции и могут применяться к новым изображениям. Если набор признаков меняется, то необходимо обучать регрессию заново с нуля.
Свойства зёрен можно изучать с помощью нескольких функций. Простейшей из них является сводная информация о зёрнах
→ →
Эта функция рассчитывает общее число помеченных зёрен, их общую площадь (площадь проекции) как в виде абсолютного значения, так и в виде доли общей площади поля данных, общий объём зёрен, общую длину границ зёрен, среднюю площадь и сторону эквивалентного квадрата для отдельного зерна. Средний размер рассчитывается усреднением стороны эквивалентного квадрата, и его квадрат в общем случае не будет равным средней площади.
Общие характеристики области под маской могут быть получены с помощью инструмента «статистические величины» когда включена опция Использовать маску. Если инвертировать маску та же информация может быть получена об областях вне зёрен.
→ →
Функция статистики зёрен показывает среднее, срединное, стандартное отклонение (среднеквадратичное) и межквартильный диапазон для всех доступных свойств зёрен в одной таблице.
→ →
Распределения зёрен является наиболее мощным и сложным инструментом. Он работает в двух режимах: построение графиков и экспорт необработанных данных. В режиме построения графиков выбранные характеристики отдельных зёрен, рассчитываются, собираются, и строятся в виде суммарных графиков, показывающих их распределения.
Экспорт необработанных данных полезен для экспертов, которым нужно, например, рассчитывать корреляцию характеристик отдельных зёрен. В этом режиме выбранные характеристики зёрен рассчитываются и записываются в виде таблицы в текстовый файл, где каждая строка соответствует отдельному зерну, а столбцы соответствуют выбранным величинам. Порядок следования столбцов тот же, что и порядок следования величин в диалоговом окне; все величины записывается в единицах измерения СИ, что является общепринятым в Gwyddion.
→ →
Корреляция зёрен строит график одной выбранной величины зёрен как функцию другой величины, показывая корреляции между ними.
Инструмент измерения зёрен является интерактивным способом получения той же информации об отдельных зёрнах, что и Распределения зёрен в режиме экспорта необработанных данных. После выбора зерна мышью в окне данных, все доступные величины показываются в окне инструмента.
Помимо физических характеристик, этот инструмент также показывает номер зерна. Номера зёрен соответствуют номерам строк (начиная с 1) в файлах, экспортированных инструментом распределений зёрен.
Инструменты распределений зёрен и измерения зёрен могут рассчитывать следующие свойства зёрен:
- Свойства значений
- Минимум, минимальное значение (высота), найденное внутри зерна.
- Максимум, максимальное значение (высота), найденное внутри зерна.
- Среднее, среднее всех значений внутри зерна, средняя высота зерна.
- Срединное, срединное всех значений внутри зерна, срединная высота зерна.
- Ср. квадр., стандартное отклонение для всех значений, встретившихся внутри зерна.
- Минимум на границе, минимальное значение (высота) найденное на внутренней границе зерна, т.е. внутри множества точек, лежащих внутри зерна, но по крайней мере одна из соседних точек которых лежит вне зерна.
- Максимум на границе, максимальное значение (высота) найденное на внутренней границе зерна, т.е. внутри множества точек, лежащих внутри зерна, но по крайней мере одна из соседних точек которых лежит вне зерна.
- Свойства площадей
- Площадь проекции, площадь проекции зерна на плоскость.
- Сторона эквивалентного квадрата, сторона квадрата с той же площадью проекции, что и у зерна.
- Радиус эквивалентного диска, радиус диска с той же площадью проекции, что и у зерна.
- Площадь поверхности, площадь поверхности зерна, см. раздел статистические величины для описания метода оценки площади поверхности.
- Площадь выпуклой оболочки, площадь проекции выпуклой оболочки зерна. Площадь выпуклой оболочки несколько больше площади зерна даже для достаточно выпуклых зёрен вследствие пикселизации маски. Точно такую же площадь зерна, как и площадь проекции выпуклой оболочки, будут иметь только зёрна в виде прямоугольников.
- Свойства границы
- Длина границы проекции, длина проекции границы зерна на горизонтальную плоскость (а не на реальную трёхмерную поверхность). Метод оценки длины границы описан ниже.
- Минимальный ограничивающий размер, минимальный размер зерна в горизонтальной плоскости. Может быть показан как минимальная ширина зазора в горизонтальной плоскости, через который может пройти зерно.
- Направление минимального ограничивающего размера, направление зазора из описания предыдущей величины. Если зерно обладает симметрией, при которой таких направлений несколько, выбирается одно из них.
- Максимальный ограничивающий размер, максимальный размер зерна в горизонтальной плоскости. Может быть показан как максимальная ширина зазора в горизонтальной плоскости, который можно заполнить зерном.
- Направление максимального ограничивающего размера, направление зазора из описания предыдущей величины. Если зерно обладает симметрией, при которой таких направлений несколько, выбирается одно из них.
- Максимальный радиус вписанного диска, радиус максимального диска, который помещается внутри зерна. Должен поместиться полный диск, а не ограничивающая его окружность, что имеет значение для зёрен с пустотами внутри. Можно использовать Инструмент редактирования маски чтобы заполнить пустоты в зёрнах и избавиться от них.
- Положение центра по x максимального вписанного диска, горизонтальная координата центра максимального вписанного диска. Точнее, одного такого диска, если он не уникален.
- Положение центра по y максимального вписанного диска, вертикальная координата центра максимального вписанного диска. Точнее, одного такого диска, если их несколько, и того же, что и у предыдущего элемента.
- Минимальный радиус описанной окружности, радиус минимальной окружности, целиком содержащей зерно.
- Положение центра по x минимальной описанной окружности, горизонтальная координата центра минимальной описанной окружности.
- Положение центра по y минимальной описанной окружности, вертикальная координата центра минимальной описанной окружности.
- Средний радиус, среднее расстояние от центра масс зерна до его границы. Это свойство в основном имеет смысл только для выпуклых или почти выпуклых зёрен.
- Минимальный диаметр Мартина, минимальная длина срединной линии, проходящей через зерно.
- Направление минимального диаметра Мартина, направление линии из предыдущего пункта. Если у зерна проявляется симметрия и таких направлений несколько, то из них произвольно выбирается одно.
- Максимальный диаметр Мартина, максимальная длина срединной линии, проходящей через зерно.
- Направление максимального диаметра Мартина, направление линии из предыдущего пункта. Если у зерна проявляется симметрия и таких направлений несколько, то из них произвольно выбирается одно.
- Свойства объёмов
- Объём между нулевой плоскостью и поверхностью, объём между поверхностью зерна и плоскостью z = 0. Значения ниже нуля формируют отрицательные объёмы. Уровень нуля должен быть установлен на разумное значение чтобы получать вменяемые результаты (нередко достаточно Исправить нуль), что является достоинством этого метода: можно использовать базисную плоскость по выбору.
- Объём между поверхностью и плоскостью, проходящей через минимум, объём между поверхностью зерна и плоскостью z = zmin, где zmin - минимальное значение (высота), найденное внутри зерна. Этот метод учитывает окружающую зерно поверхность, но обычно недооценивает объём, особенно для малых зёрен.
- Объём между поверхностью и фоном, вычисленным по Лапласу, объём между поверхностью зерна и базовой поверхностью, образованной интерполяцией окружающей зерно поверхности по Лапласу. Другими словами, это объём. который исчезнет после использования инструментов Интерполировать данные под маской или удаления зёрен с лапласовой интерполяцией зерна. Это один из наиболее сложных методов, с другой стороны его результаты труднее всего предугадать.
- Свойства расположения
- Положение центра по x, горизонтальная координата центра зерна. Поскольку площадь зерна определяется как площадь под соответствующими точками маски, центр зерна размером с пиксель будет иметь полуцелые координаты, не целые. Смещение начала координат поля данных учитывается (если оно есть).
- Положение центра по y, вертикальная координата центра зерна. Интерпретация описана выше.
- Свойства наклонов
- Свойства, относящиеся к кривизне
- Центр кривизны по x, горизонтальное положение центра квадратичной поверхности, которой аппроксимируется поверхность зерна.
- Центр кривизны по y, вертикальное положение центра квадратичной поверхности, которой аппроксимируется поверхность зерна.
- Центр кривизны по z, значение в центре квадратичной поверхности, которой аппроксимируется поверхность зерна. Следует отметить, что это значение на аппроксимирующей поверхности, не на поверхности зерна.
- Кривизна 1, меньшая кривизна (т.е. значение, обратное радиусу кривизны) в центре.
- Кривизна 2, большая кривизна (т.е. значение, обратное радиусу кривизны) в центре.
- Угол кривизны 1, направление, соответствующее радиусу Кривизна 1.
- Угол кривизны 2, направление, соответствующее радиусу Кривизна 2.
- Свойства, относящиеся к моментам
- Большая полуось эквивалентного эллипса, длина большей полуоси эллипса, у которого будет такой же угловой момент второго порядка в горизонтальной плоскости.
- Малая полуось эквивалентного эллипса, длина меньшей полуоси эллипса, у которого будет такой же угловой момент второго порядка в горизонтальной плоскости.
- Ориентация эквивалентного эллипса, направление большей полуоси эллипса, у которого будет такой же угловой момент второго порядка в горизонтальной плоскости. Для круглого зерна, этот угол устанавливается в ноль по определению.
Длина границы зерна оценивается путём суммирования оценочного вклада каждой комбинации из четырёх точек границы. Вклады показаны на следующем рисунке для каждого вида конфигурации, где hx и hy - размеры пикселей вдоль соответствующих осей и h - длина диагонали пикселя:
Вклады соответствуют один в один длинам сегментов границы многоугольника, которым аппроксимируется форма зерна. Построение эквивалентной формы многоугольника также показано на этом рисунке.
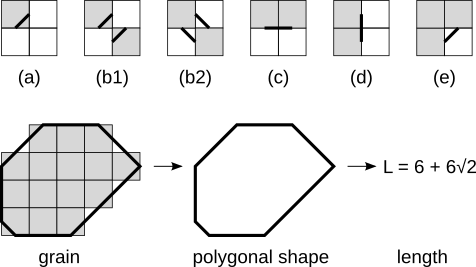
Вклад конфигураций пикселей в оцениваемую длину поверхности (сверху). Серые квадраты представляют пиксели внутри зерна, белые - внешние пиксели. Оценочный вклад каждой конфигурации: (a) h/2, (b1), (b2) h, (c) hy, (d) hx, (e) h/2. Случаи (b1) и (b2) отличаются только формой сегментов-многоугольников, оценочные длины поверхности одинаковы. Нижняя часть рисунка показывает, как сегменты объединяются, чтобы образовать многоугольник.
Объём зерна после вычета основания, оценивается как объём точно такой же фигуры, верхняя поверхность которой использовалась для расчёта площади поверхности. Следует отметить, что для объёма, ограниченного многогранником, метод эквивалентен классическому двумерному методу интегрирования с помощью трапеций. Однако, мы рассчитываем объём под маской с центрами на гранях фигуры, поэтому их вклад в интеграл распределён иначе, как показано на рисунке ниже.
Относящиеся к кривизне значения для отдельных зёрен считаются так же, как и общая кривизна, рассчитываемая функцией Кривизна. См. описание функции для более подробной информации.
Вписанные диски и описанные окружности зёрен можно визуализировать используя функции → → и → → . Эти функции создают круговые выделенные области, представляющие соответствующие диски или окружности для каждого зерна. которые затем можно показать с помощью инструмента Менеджер выделенных областей.
Диаметр Мартина это длина особой линии, проходящей через зерно в заданном направлении, которая делит площадь зерна на две равные части (срединная линия). Эта величина в основном полезна для зёрен которые являются более или менее выпуклыми. Для справки мы должны отметить, что если зерно является сильно не-выпуклым и срединная линия пересекает его несколько раз, Gwyddion суммирует длины сегментов, которые лежат внутри зерна (другим вариантом могло бы быть просто взять расстояние между первым и последним пересечением).
Помеченные зёрна можно фильтровать по порогу любой из доступных для зёрен величин используя меню → → . Этот модуль можно использовать для основных операций, таких как удаление слишком мелких зёрен используя порог площади в пикселях, а также для сложной фильтрации, использующей логические операции над несколькими величинами, относящимися к параметрам зёрен.
Фильтр сохраняет зёрна, которые удовлетворяют условию, заданному как Оставлять зёрна, удовлетворяющие и удаляет все остальные. Условие задаётся как логическое выражение, содержащее от одного до трёх пороговых условий, обозначенных как A, B и C. Простейшее условие это просто A, означающее, что величина A должна лежать между заданными порогами.
Каждое условие состоит из верхнего и нижнего порога для одной величины, относящейся к зёрнам, например, площади в пикселях или значению минимума. Значения должны лежать в диапазоне [нижний,верхний] чтобы удовлетворить условию и тем самым сохранить это зерно. Следует отметить, что можно выбрать нижний порог больше верхнего. В этом случае условие инвертируется, т.е. зерно сохраняется если значение лежит вне диапазона [нижний,верхний].
Отдельные величины для зёрен присваиваются A, B и C выбором величины из списка и нажатием на соответствующую кнопку в Установить выбранное как. Текущий выбранный набор величин показан в заголовках Условие A, Условие B и Условие C.
→ →
Когда изображения с выделенными зёрнами в дальнейшем обрабатываются в другом программном обеспечении, может оказаться полезным в явном виде определь какой номер зерна присвоен какой области в Gwyddion. Эта функция создаёт избражение, где каждый пиксель содержит соответствующий номер зерна. Следовательно, хотя данные при этом по прежнему будут представлены вещественными числами, они будут на самом деле целыми.
Зёрна можно выровнять по вертикали используя функцию → → . Эта функция сдвигает каждое зерно таким образом, чтобы сделать одну из связанных с высотой величин всех зёрен одинаковой. Обычно выравниваются минимальные значения внутри зерна, но возможны другие варианты.
Данные между зёрнами также сдвигаются по вертикали. Эти сдвиги интерполируются из сдвигов зёрен используя уравнение Лапласа, что приводит к плавным переходам сдвигов между зёрнами (хотя и не принимая во внимания другие особенности поверхности).
[1] P. Klapetek, I. Ohlídal, D. Franta, A. Montaigne-Ramil, A. Bonanni, D. Stifter, H. Sitter: Atomic force microscopy characterization of ZnTe epitaxial films. Acta Physica Slovaca 53 (2003) 223–230, doi:10.1143/JJAP.42.4706
[2] Luc Vincent and Pierre Soille: Watersheds in digital spaces: an efficient algorithm based on immersion simulations. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13 (1991) 583–598, doi:10.1109/34.87344