При анализе случайно шероховатых поверхностей нередко требуется статистический подход для определения набора описывающих эту поверхность величин. В Gwyddion реализовано несколько различных подходов как это можно сделать. В этом разделе мы опишем различные статистические инструменты и модули, представленные в Gwyddion, а также представим основные формулы, которые использовались для разработки лежащих в их основе алгоритмов.
Данные сканирующей зондовой микроскопии обычно представляются как двумерное поле данных размера N×M где N и M – число строк и столбцов поля данных, соответственно. Настоящая площадь этого поля обозначается как Lx×Ly, где Lx и Ly – размеры вдоль соответствующих осей. Интервал дискретизации (расстояние между двумя соседними точками в скане) обозначается Δ. Мы предполагаем, что интервал дискретизации одинаков как в x, так и в y-направлении и что высота поверхности в заданной точке (x, y) может быть описана случайной функцией ξ(x, y) с заданными статистическими свойствами.
Следует заметить, что данные АСМ обычно собираются как линейные сканы вдоль оси x, которые объединяются вместе, чтобы сформировать двумерное изображение. Следовательно, скорость сканирования в направлении x значительно больше, чем скорость сканирования вдоль оси y. В результате, статистические свойства данных АСМ обычно собираются вдоль профилей, параллельных оси x, поскольку на них меньше влияет низкочастотный шум и температурный дрейф образца.
Статистические величины включают в себя основные свойства распределения значений высоты, включая его дисперсию, коэффициент асимметрии и эксцесс. Величины, доступные в меню инструмента Статистические величины программы Gwyddion, разделены на несколько групп.
Основанные на моментах величины выражаются через интегралы функции распределения высот с некоторыми степенями высоты. Они включают в себя привычные величины:
- Среднее значение.
- Среднеквадратичное значение или СКВ неровностей высоты Sq: это значение вычисляется из второго центрального момента значений данных.
- Значение среднеквадратичного отклонения зерён которое будет отличаться от обычного среднеквадратичного только при использовании маски. Среднее значение при этом определяется отдельно для каждого зерна (непрерывной части маски или инвертированной маски, в зависимости от типа маскирования) и дисперсия затем вычисляется относительно этих средних для зёрен значений.
- Средняя шероховатость или Sa нерегулярностей высоты.
- Коэффициент асимметрии распределения высот рассчитывается из третьего центрального момента значений данных.
- Эксцесс распределения высот рассчитывается из четвёртого центрального момента значений данных.
Точнее, среднеквадратичное отклонение (σ), коэффициент асимметрии (γ1), и эксцесс (γ2) вычисляются из центральных моментов i-того порядка μi
где z̄ обозначает среднее значение. Они выражаются следующими формулами:
Следует отметить, что Gwyddion рассчитывает избыточный эксцесс, который будет равен нулю для гауссова распределения. Добавьте 3 если вам нужен параметр текстуры области Sku.
Средняя шероховатость Sa похожа на значение среднеквадратичного отклонения, отличие состоит в том, что она рассчитывается как сумма модулей разности между значением данных и средним, вместо квадратов разности.
Порядковые величины представляют собой значения, соответствующие определённому положению если все значения будут упорядочены. Они включают в себя:
- Минимум, максимум, срединное значение.
- Максимальная высота пика Sp, которая отличается от максимума тем, что рассчитывается относительно средней высоты.
- Максимальная глубина впадины Sv, которая отличается от минимума тем, что рассчитывается относительно средней высоты.
- Максимальная высота Sz, полный диапазон значений. Это общая разность между минимумом и максимумом или, что то же самое, между Sv и Sp.
Гибридные величины комбинируют высоты и пространственные отношения в плоскости поверхности и включают в себя:
- Площадь проекции и площадь поверхности: подсчитывается простой триангуляцией.
- Объём, рассчитанный как интеграл высоты поверхности по области, покрытой маской.
- Средний уклон граней в области: вычисляется усреднением нормализованных векторов направления граней.
- Вариация, которая рассчитывается как интеграл модуля локального градиента.
- Наклон поверхности, определяется как среднеквадратичный локальный градиент. Другими словами, сначала вычисляется среднеквадратичное значение локального градиента. Наклон затем получается как корень из этого числа.
Площадь поверхности оценивается следующим методом. Пусть zi для i = 1, 2, 3, 4 обозначает значения в четырёх соседних точках (центрах пикселей), а hx и hy - размеры пикселей вдоль соответствующих осей. Если дополнительная точка помещается в центр прямоугольника который соответствует общему углу четырёх пикселей (используя среднее значение четырёх пикселей), образуются четыре треугольника и площадь поверхности может быть приближенно оценена суммированием их площадей. Это приводит к следующим формулам для площади одного треугольника (верхняя) и площади поверхности для одного пикселя (нижняя):
Теперь этот метод хорошо определён для внутренних точек области. Каждое значение участвует в восьми треугольниках, по два с каждым из четырёх соседних значений. Половина из этих треугольников лежит внутри одного пикселя, другая половина в другом пикселе. Подсчётом площади, лежащей внутри каждого пикселя, общая площадь определяется также для зерён и областей под маской. Осталось определить её для граничных пикселей всего поля данных. Мы это делаем виртуально расширяя поле данных копией граничного ряда пикселей с каждой стороны для расчёта площади поверхности, таким образом делая все интересующие нас пиксели внутренними.
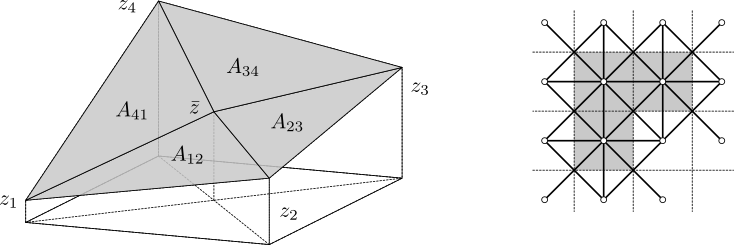
Схема триангуляции при рассчёте площади поверхности (слева). Применение схемы триангуляции (справа) к области под маской из трёх пикселей, т.е. зерну. Малые круги обозначают вершины в центрах пикселей zi, тонкие пунктирные линии обозначают границы пикселей, толстыми линиями показано разбиение на треугольники. Оценка площади поверхности равна области под маской (серой) на этой схеме.
Дополнительно инструмент рассчитывает некоторые значения, которые трудно отнести к какой-то из предыдущих категорий:
- Нессответствие линий скана, характеризующая различия между линиями скана. Оно может быть показано следующим образом: если каждая линия изображения будет заменена средним двух соседних линий, новое изображение будет немного отличаться от оригинального. Взяв среднеквадратичную разницу и поделив на среднеквадратичное значение изображения, мы получаем показываемое значение несоответствия.
Подсказка
По умолчанию инструмент «Статистические величины» показывает значения для всего изображения. Если вам нужно исследовать определённую область внутри изображения, просто щёлкните мышью и обведите её прямоугольником. Окно инструмента обновится с новыми значениями основанными на новой области. Если вы снова хотите просмотреть статистику для всего изображения, щёлкните один раз на окне данных и инструмент сбросится в исходное состояние.Одномерные статистические функции доступны при использовании инструмента Статистические функции. В окне инструмента можно выбрать, какую функцию нужно рассчитать, используя выпадающий список слева, озаглавленный Тип вывода. Предпросмотр графика будет обновляться автоматически. Можно выбрать направление, в котором будут рассчитываться функции (горизонтальное или вертикальное), но, как уже говорилось выше, мы рекомендуем использовать направление быстрой оси сканирования. Также можно выбрать, какой из методов интерполяции использовать. После того, как выбор закончен, можно нажать кнопку чтобы закрыть окно инструмента и вывести новое окно графика, которое содержит статистические данные.
Подсказка
Подобно инструменту Статистические величины, этот инструмент оценивает по умолчанию всё изображение, но при желании можно выбрать область, на которой будет проводиться анализ.Простейшими статистическими функциями являются функции распределения высот и наклонов. Они могут быть рассчитаны как неинтегральные (т.е. плотности) и как интегральные. Эти функции рассчитываются как нормированные гистограммы значений высоты или наклона (полученного как производные в выбранном направлении – горизонтальном или вертикальном). Другими словами, величина по абсциссе в «распределении углов» – тангенс угла, а не сам угол.
Нормировка плотностей ρ(p) (где p – соответствующая величина, высота или наклон) такова, что
Очевидно, что масштаб значений при этом не зависит от числа точек данных и числа выборок в гистограмме. Интегральные распределения – интегралы плотностей и они принимают значения из интервала [0, 1].
Величины распределений высот и углов относятся к статистическим величинам первого порядка, описывающих только статистические свойства отдельных точек. Однако, для полного описания свойств поверхности необходимо изучать функции более высоких порядков. Обычно применяются статистические величины второго порядка, описывающие взаимные соотношения пар точек на поверхности. К этим функциям относятся функция автокорреляции, функция корреляции высота-высота и функция спектральной плотности мощности. Далее следует описание каждой из них:
Функция автокорреляции задаётся как
где z1 и z2 – значения высоты в точках (x1, y1), (x2, y2); при этом τx = x1 − x2 и τy = y1 − y2. Функция w(z1, z2, τx, τy) обозначает двумерную плотность вероятности случайной функции ξ(x, y), соответствующей точкам (x1, y1), (x2, y2) и расстоянию между этими точками τ.
Из дискретных данных АСМ можно извлечь эту функцию в виде
где m = τx/Δx, n = τy/Δy. Следовательно, эта функция может быть рассчитана для дискретного набора значений τx и τy, разделённых интервалами дискретизации Δx и Δy, соответственно.
Для измерений АСМ мы обычно рассчитываем одномерную функцию автокорреляции основанную на профилях вдоль оси быстрого сканирования. Следовательно, она может рассчитываться из дискретных данных АСМ как
Одномерная функция автокорреляции нередко считается имеющей форму гауссовой, т.е. заданной следующим соотношением:
где σ обозначает среднеквадратичное отклонение высот и T обозначает длину автокорреляции.
Для экспоненциальной функции автокорреляции у нас получается следующее соотношение
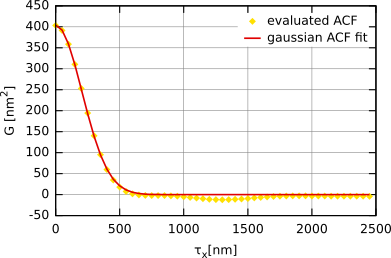
Функция автокорреляции, полученная для модели гауссовой случайной шероховатой поверхности (т.е. с гауссовой функцией автокорреляции) с σ ≈ 20 nm и T ≈ 300 nm.
Мы можем также ввести радиально усреднённую функцию автокорреляции Gr(τ), т.е. усреднённую вдоль заданного углом направления двумерную функцию автокорреляции, которая, естественно, содержит ту же самую информацию, что и одномерная функция автокорреляции для изотропных поверхностей:
Примечание
Для оптических измерений (т.е. спектроскопической рефлектометрии, эллипсометрии) гауссова функция автокорреляции обычно ожидается достаточно хорошо совпадающей со свойствами поверхности. Однако, некоторые статьи, связанные с ростом поверхности и окислением, обычно предполагают, что экспоненциальная форма ближе к реальности.Функция распределения границы (ФРГ) это вторая производная от АКФ
Положения и знаки её экстремумов связаны со значениями вроде размера зёрен и межзёренных расстояний.
Различие между функцией корреляции высота-высота и функцией автокорреляции очень мало. Как и в случае с функцией автокорреляции, мы суммируем произведение двух различных значений. Для функции автокорреляции эти значения представляют различные расстояния между точками. Для функции корреляции высота-высота мы вместо этого используем степень разности между точками.
Для измерений АСМ мы обычно рассчитываем одномерную функцию корреляции высота-высота, основанную только на профилях вдоль быстрой оси сканирования. Следовательно, она может быть рассчитана из дискретных значений данных АСМ как
где m = τx/Δx. Таким образом, функция может быть рассчитана на дискретном наборе значений τx разделённом интервалом дискретизации Δx.
Одномерная функция корреляции высота-высота нередко считается имеющей форму гауссовой, т.е. заданной следующим соотношением:
где σ обозначает среднеквадратичное отклонение высот и T обозначает длину автокорреляции.
Для экспоненциальной функции корреляции высота-высота у нас получается следующее соотношение
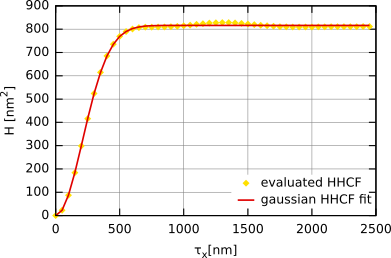
На следующем рисунке функция корреляции высота-высота построена для модели гауссовой поверхности. Она аппроксимирована формулой, приведённой выше. Результирующие значения σ и T полученные аппроксимацией функцией корреляции высота-высота практически те же, что и для функции автокорреляции.
Двумерная функция спектральной плотности мощности может быть записана в терминах преобразования Фурье от функции автокорреляции
Подобно функции автокорреляции, мы также обычно рассчитываем одномерную функцию спектральной плотности мощности, которая задана уравнением
Эта функция может быть расчитана с помощью быстрого преобразования Фурье следующим образом:
где Pj(Kx) – коэффициент Фурье для j-той строки, т.е.
Если мы выберем гауссову функцию автокорреляции, соответствующее гауссово соотношение для функции спектральной плотности мощности будет следующим:
Для поверхности с экспоненциальной функцией автокорреляции мы имеем
На следующем рисунке построены результирующая функция спектральной плотности мощности и её аппроксимация для той же самой поверхности, что использовалась для функции автокорреляции и функции корреляции высота-высота. Можно видеть, что функция может быть снова аппроксимирована гауссовой функцией спектральной плотности мощности. Результирующие значения σ и T практически те же самые, что и для аппроксимации функции автокорреляции и функции корреляции высота-высота.
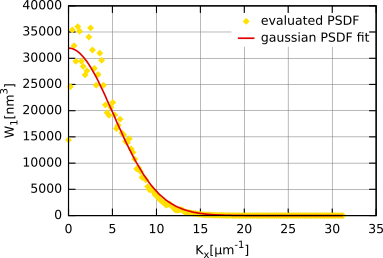
Функция спектральной плотности мощности полученная для данных, смоделированных с гауссовой функцией автокорреляции.
Мы можем также ввести радиальную функцию спектральной плотности мощности Wr(K), т.е. интегрированную вдоль заданного углом направления двумерную функцию спектральной плотности мощности, которая, естественно, содержит ту же самую информацию, что и одномерная функция спектральной плотности мощности для изотропных шероховатых поверхностей:
Для поверхности с гауссовой функцией автокорреляции эта функция может быть выражена как
для поверхностей с экспоненциальной как
Подсказка
В Gwyddion можно аппроксимировать все представленные здесь статистические функции их гауссовыми и экспоненциальными формами. Чтобы это сделать, сначала нажмите в окне инструмента Статистические функции. При этом будет создано новое окно графика. При выбранном этом окне, нажмите на → .Спектральная плотность также может интегрироваться в радиальном направлении, давая угловой спектр. Его пики могут быть использованы для определения основных направлений в текстуре изображения.
Функционалы Минковского используются для описания глобальных геометрических характеристик структур. Двумерный дискретный вариант объема V, поверхности S и связности (характеристики Эйлера – Пуанкаре) χ рассчитываются в соответствии со следующими формулами:
Здесь N обозначает общее число пикселей, Nwhite обозначает число «белых» пикселей, пикселей выше порога. Пиксели, которые ниже порога, называются «чёрными». Символ Nbound обозначает число границ между чёрными и белыми пикселями. И, наконец, Cwhite и Cblack обозначают число непрерывных наборов белых и чёрных пикселей, соответственно.
Для изображений с непрерывным набором значений функционалы параметризованы по значению порога высоты ϑ, который отделяет белые пиксели от чёрных, т.е. они могут рассматриваться как функции этого параметра. И эти функции V(ϑ), S(ϑ) и χ(ϑ) строятся.
Распределение диапазонов это график роста диапазона значений от пространственного расстояния. Это всегда неубывающая функция.
Для каждого пикселя изображения и каждого расстояния по горизонтали можно рассчитать минимальное и максимальное из значений, которые лежат не далее заданного расстояния от выбранного пикселя. Локальный диапазон это разность между максимумом и минимумом (и в двумерном случае может быть показано используя функцию презентации Ранга). Усреднение локальных диапазонов для всех пикселей изображения даёт кривую распределения диапазонов
График функции относительной площади показывает отношение площади развитой поверхности и площади проекции за вычетом единицы как функцию от масштаба, на котором рассчитывается площадь поверхности. Из за вычета единицы, которой равно отношение для полностью плоской поверхности, величина называется «избыточной» площадью.
Подобно функциям корреляции, избыточная площадь может быть определена как направленная величина. Однако, функция, показанная в иструменте, предполагает изотропную поверхность, горизонтальное или вертикальное направление, которые можно выбрать, задают только основное направление, используемое в расчёте.
Большая часть статистических функций поддерживает использование масок. Другими словами, они могут быть рассчитаны для областей изображения произвольной формы. Для некоторых из них, таких как распределение высот или углов, не требуется дополнительных пояснений: в расчёте используются только пиксели изображения под (или не под) маской. Однако, смысл функции менее ясен для функций корреляции и спектральных плотностей.
Мы покажем его для автокорреляционной функции (простейший случай). Полное описание можно найти в литературе [1]. Формула для дискретной автокорреляционной функции может быть переписана как
где Ωm это набор пикселей изображения внутри области для которой пиксель m столбцов правее также лежит внутри области. если мы рассчитываем функцию автокорреляции для прямоугольной области, например для всего изображения, ничего не меняется. Однако, данная формула достоверно задаёт функцию для областей любой формы. Осталось только понять, как можно эффективно проводить такой расчёт.
Для этого мы определяем ck,l как маску нужных пикселей, которая равна 1 для пикселей, которые мы хотим включить и 0 для пикселей, которые мы исключаем из расчёта. Из этого следует что
Далее, если данные изображения перед расчётом умножить на ck,l то сумму автокорреляционной функции для неправильной области можно заменить на обычную сумму автокорреляционной функции по всему изображению. И то, и другое можно эффективно рассчитывать с помощью быстрого преобразования Фурье.
Важно отметить, что количество информации, доступной в данных об автокорреляционной функции для заданной m зависит от Ωm. В отличие от прямоугольных изображений, она не должна монотонно убывать с увеличением m и может меняться произвольным образом. Там могут быть даже вырезы, т.е. горизонтальные интервалы m для которых область не содержит пар пикселей с нужным расстоянием между ними. Если это происходит, то Gwyddion заменяет отсутствующие значения используя линейную интерполяцию.
Функция корреляции высота-высота рассчитывается подобным образом, только суммы должны быть разбиты на части, которые затем рассчитываютсяя с использованием БПФ. Для ФСПМ это невозможно поскольку каждый коэффициент в разложении Фурье зависит от каждого значения данных. Таким образом, вместо этого, рассчитывается циклическая автокорреляционная функция таким же образом, как АКФ, а ФСПМ получается как результат её преобразования Фурье.
Инструмент Статистики по строкам/столбцам рассчитывает численные характеристики каждой строки или столбца и строит их как функции его/её положения. Это делает его в некоторой степени дополнительным к инструменту Статистические функции. Доступные величины включают в себя:
- Среднее значение, минимум, максимум, срединное значение.
- Среднеквадратичное значение неровностей высоты: это значение вычисляется из дисперсии данных Rq..
- Коэффициент асимметрии и эксцесс распределения высот.
- Длина линии поверхности. Эта величина оценивается как общая длина прямых сегментов, соединяющих значения данных в строке (столбце).
- Общий уклон, т.е. тангенс средней линии, аппроксимирующей строку (столбец).
- Тангенс β0. Это характеристика крутизны локальных уклонов, близко связанная с поведением функций автокорреляции и корреляции высота-высота в нуле. Для дискретных значений она вычисляется следующим образом:
- Стандартные параметры шероховатости Ra, Rz, Rt.
В дополнение к графику, показывающему значения для индивидуальных строк/столбцов, среднее значение и среднеквадратичное отклонение выбранной величины рассчитывается из набора отдельных значений для строк/столбцов. Следует подчеркнуть, что стандартное отклонение выбранной величины представляет собой разброс значений для отдельных строк/столбцов и не может рассматриваться как ошибка аналогичной двумерной величины.
Инструмент длина корреляции можно использовать для быстрой оценки длины автокорреляции изображения T на основе линий скана. Длина автокорреляции оценивается с использованием нескольких распространенных методов. Показываются результаты сразу всех методов, что позволяет выбрать наиболее подходящий (и сразу сравнить насколько расчёты по разным методам отличаются).
- Наивное затухание АКФ до 1/e
- Горизонтальное расстояние, на котором дискретная одномерная АКФ затухает до 1/e от своего максимального значения (которое она достигает в нуле). Это общепринятое определение, соответствующее также выражениям для гауссовой и экспоненциальной АКФ.
- Экстраполированное затухание АКФ до 1/e
- Наивная оценка будет смещена. Простой и более-менее свободный от предположений метод коррекции это экстраполяция на бесконечно длинную линию сканирования зная известные асимптотические зависимости от длины линии сканирования [2,3]. Это результат подобной экстраполяции.
- Затухание АКФ до нуля
- Горизонтальное расстояние, на котором дискретная одномерная АКФ затухает до нуля. Не часто встречающаяся, но иногда полезная характеристика затухания АКФ.
- Аппроксимация ФСПМ гауссианой
- Длина автокорреляции полученная аппроксимацией оценка одномерной ФСПМ используя модель гауссовой автокорреляции. Оценка будет иметь смысл только если АКФ шероховатости действительно близка к гауссовой.
- Аппроксимация ФСПМ экспонентой
- Длина автокорреляции полученная аппроксимацией оценки одномерной ФСПМ используя модель экспоненциальной автокорреляции. Оценка будет иметь смысл только если АКФ шероховатости действительно близка к экспоненциальной.
Инструмент также показывает отношение между длиной автокорреляции T и размером изображения L (или точнее длиной линии сканирования).
- Отношение α = T/L
- Это отношение используется для оценки отклонения параметров шероховатости вследствие конечной области измерения [2,3]. Длина автокорреляции берётся из экстраполяции затухания.
- Размер изображения в единицах T
- Величина, обратная α измеряет сколько длин автокорреляции помещается в одну линию сканирования. Она несёт ту же информацию, но воспринимается проще.
Грубая оценка отклонения может быть получена следующим образом. Она в основном полезна чтобы оценить является ли размер скана достаточным или насколько результат может иметь отклонение - попытки использовать её для коррекции легко могут сделать всё ещё хуже.
- Оценить α – например, с помощью данного инструмента.
- Умножаем его на степень полинома, использованную при выравнивании линий сканирования плюс один. Это означает 1 для вычета среднего значения, 2 для коррекции наклона, 3 для коррекции кривизны и т.д.
- Результат оценивает относительное отклонение измеренной шероховатости. Отклонение всегда отрицательно, поэтому нужно добавить минус, если это имеет значение.
Похожая процедура может использоваться при вычете двумерного фона. Однако, почти всегда применяется один из способов выравнивания строк - как минимум неявное вычитание среднего значения. И это тогда будет основным источником отклонения.
Инструмент может проводить коррекцию линий сканирования в процессе оценки. Это управляется опцией Выравнивание линий сканирования. По умолчанию вычитается смещение, что обычно является хорошим выбором. Можно переключиться в режим отсутствия выравнивания, если нужно использовать линии скана в точности как есть. Иногда может оказаться полезно сделать быструю коррекцию наклона. Если нужны более сложные исправления или вычет более высокого порядка полинома, нужно применить их явно с помощью инструмента Выровнять строки.
→ →
Полная двумерная автокорреляционная функция введённая выше иногда используется для оценки анизотропии шероховатых поверхностей. Модуль двумерной АКФ рассчитывает функцию и может строить её сечения для выбранных направлений или рассчитывать некоторые параметры шероховатости, основанные на двумерной АКФ.
Опции на вкладке АКФ управляют тем, как функция рассчитывается и показывается. В большинстве случаев перед расчётом необходимо вычесть среднее значение (как это делает обнулить среднее значение). Это выбирается с помощью пункта Вычитание среднего значения в выравнивании данных. Однако, Выравнивание плоскости также может быть полезным. Если уровень нуля уже настроен правильно, то можно выбрать Нет для того, чтобы посчитать АКФ для неизменённых данных. Если на изображение наложена маска, диалоговое окно предлагает стандартные настройки для маски. Общее описание расчёта АКФ в случае использования маски приведено в описании статистических функций для изображений с маской.
Вкладка График содержит настройки для извлекаемых сечений АКФ. Они будут теми же, что и для обычного извлечения профилей.
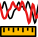
Наконец, вкладка Параметры показывает различные численные параметры, полученные из двумерной АКФ. Они определяются из затухания АКФ в различных направлениях и зависят от значения Порога, ниже которого точки данных считаются в основном не коррелирующими. Область значений выше выбранного порога помечается маской на изображении АКФ.
Порог задаётся как доля по отношению к максимуму (находящемуся в начале кооординат). В теоретических моделях длина автокорреляции соответствует затуханию АКФ до 1/e. Это также будет значением по умолчанию. Однако, в стандартах, описывающих шероховатость, он обычно выбирается равным 0,2. Для того, чтобы результаты можно было сравнивать, убедитесь, что вы используете везде одно и то же значение порога.
Длина автокорреляции Sal это кратчайшее расстояние на котором АКФ спадает до значений ниже порога. Соответствующее направление также показывается, также как и направление и расстояние наиболее медленного убывания. Отношение между наибольшими и наименьшими расстояниями это текстурный коэффициент поверхности Str.
→ →
Полная двумерная функция спектральной плотности используется для оценки характеристических пространственных частот поверхностей. Модуль двумерной ФСПМ рассчитывает функцию и может строить её сечения для выбранных направлений.
Опции на вкладке ПСПМ управляют тем, как функция рассчитывается и показывается. Опция Оконной функции выбирает тип окна. Если на изображение наложена маска, диалоговое окно предлагает стандартные настройки для маски. Общее описание расчёта ФСПМ в случае использования маски приведено в описании статистических функций для изображений с маской.
Вкладка График содержит настройки для извлекаемых сечений АКФ. Они будут теми же, что и для обычного извлечения профилей.
Наконец, вкладка Параметры демонстрирует некоторый набор численных параметров, полученных на основе двумерной ФСПМ. Два из них рассчитываются используя угловой спектр: направление текстуры Std и индекс направления текстуры Stdi. Std задаётся направлением, в котором интеграл радиальной ФСПМ будет наибольшим и определяет основное направление текстуры. Stdi измеряет насколько данное направление доминирует над остальными сравнивая среднее значение по всем направлениям с основным направлением. Следует заметить, что меньшее значение Stdi соответствует большему весу основного направления (не меньшему).
Несколько функций в меню → оперируют статистикой двухмерных наклонов (производных).
рассчитывает простое двухмерное распределение производных, то есть горизонтальные и вертикальные координаты результирующего поля данных это, соответственно, горизонтальные и вертикальные производные. Наклоны могут быть посчитаны как центральные производные (односторонние на границах изображения) или, если включена опция Использовать аппроксимацию локальной плоскостью, аппроксимацией локальной плоскостью окрестности каждой точки и использованием её градиента.
также может строить суммарные графики, представляющие одномерные распределения величин, относящихся к локальным уклонам и углам наклона граней задаваемым следующими уравнениями:
Доступны три различных графика:
- , распределение угла наклона ϑ относительно горизонтальной плоскости. Естественно, что представление наклона в виде угла требует чтобы значения и пространственные координаты были одними физическими величинами.
- напоминает график ϑ за исключением того, что строится распределение производной v вместо угла.
- показывает интеграл v2 для каждого направления φ в горизонтальной плоскости. Это означает, что данная величина не просто распределение φ , поскольку области с большими уклонами вносят больший вклад, чем плоские области.
Функция - инструмент визуализации, который не рассчитывает распределение в строгом смысле. Для каждой производной v строится круг точек, удовлетворяющих уравнению
Число точек на круге задаётся параметром Число шагов.
→ →
Эта функция может оценивать дифференциальную энтропию распределений значений и уклонов, а также показывает визуализацию как она рассчитывается.
Дифференциальная энтропия Шеннона для функции плотности вероятности может быть выражена как
где X — область определения переменной x. Например, для распределения высоты x представляет высоту поверхности и X будет всей действительной осью. Для распределения углов x это двухкомпонентный вектор, состоящий из производных по осям и X, соответственно, будет плоскостью.
Существует большое количество более или менее сложных методов оценки энтропии. Gwyddion использует относительно простой метод, основанный на гистограмме, в котором приведённая выше формула аппроксимируется с помощью
где pi и wi — оценки плотности вероятности, т.е. нормализованное значение гистограммы и ширина i-той корзины гистограммы.
Естественно, оцениваемое значение энтропии зависит от выбора ширины корзины, за исключением равномерного распределения, где оценка от этого не зависит. Из этого следует, что для разумных распределений подходящей шириной корзины будет такая, при которой оценка энтропии не меняется при небольшом изменении ширины. Это и будет критерием выбора подходящей ширины корзины.
На практике это означает, что энтропия оценивается для большого диапазона вариантов ширины корзины (обычно много порядков величины), получая масштабную кривую, показываемую в виде графика в правой части диалогового окна. Энтропия после этого оценивается путём определения точки перегиба на кривой. Если такой точки нет, что может быть, например, если распределение очень близко к сумме δ-функций, в качестве энтропии будет выведено очень большое отрицательное значение.
Энтропии показываются без единиц измерения, поскольку они являются логарифмическими величинами. Для численного сравнения с другими расчётами, следует отметить, что в Gwyddion они всегда считаются из величин в основных единицах измерения СИ (т.е., например, в метрах при нанометровой шкале) и используются натуральные логарифмы. Следовательно, величины будут в естественных единицах информации (натах, nats)
Абсолютное значение энтропии зависит от абсолютной ширины распределения. Например, два гауссова распределения высот с различными значениями среднеквадратичного отклонения будут иметь различные значения энтропии. Это полезно, если мы хотим сравнивать абсолютную прямоту структур в распределении высот. С другой стороны, может оказаться полезным сравнить их способом, независимым от общего масштаба. Для этого мы можем использовать тот факт, что гауссово распределение будет иметь максимальную энтропию из всех распределений с одинаковым значением среднеквадратичного отклонения. Разница между максимальной и оцениваемой энтропией показывается как дефицит энтропии. По определению, она всегда положительна (кроме небольших отрицательных погрешностей, возникающих за счёт метода расчёта).
[1] D. Nečas and P. Klapetek: One-dimensional autocorrelation and power spectrum density functions of irregular regions. Ultramicroscopy 124 (2013) 13-19, doi:10.1016/j.ultramic.2012.08.002
[2] D. Nečas, P. Klapetek and M. Valtr: Estimation of roughness measurement bias originating from background subtraction. Measurement Science and Technology (2020) 094010, doi:10.1088/1361-6501/ab8993
[3] D. Nečas, M. Valtr and P. Klapetek: How levelling and scan line corrections ruin roughness measurement and how to prevent it. Scientific Reports 10 (2020) 15294, doi:10.1038/s41598-020-72171-8