Plusieurs algorithmes relatifs aux grains sont implémentés dans Gwyddion. On peut tout d'abord utiliser des algorithmes de seuillage (par hauteur, pente ou courbure). Ceux-ci sont très efficaces pour l'analyse de particules (pour marquer les particules présentes sur une surface plane).
→ → .
Le seuillage est la méthode la plus basique pour marquer des grains. Les seuillage par hauteur, pente et courbure sont implémentés dans ce module. Les résultats de chacune de ces méthodes de seuillage peuvent être fusionnés à l'aide de plusieurs opérateurs.
→ → . La méthode de seuillage automatique d'Otsu sépare les valeurs en deux classes, en minimisant l'écart de variance propre à chaque classe. Elle est particulièrement adaptée aux images contenant deux niveaux de valeurs relativement bien définis..
→ → ,
Cette autre fonction de marquage des grains est basée sur la détection de bord (courbure locale). L'image est traitée à l'aide d'un filtre de différence de gaussiennes d'une taille donnée, puis le seuillage est effectué sur l'image filtrée plutôt que sur l'originale.
→ → .
Les grains en contact avec les bords de l'image peuvent être éliminés à l'aide de cette fonction. Ceci peut s'avérer utile si de tels grains sont considérés comme incomplets et doivent être exclus de l'analyse. Plusieurs autres fonctions de l'outil d'édition de masque peuvent être utiles pour modifier la forme des grains après le marquage.
→ →
Dans le cas de structures plus complexes, les algorithmes de seuillage vus précédemment peuvent être inefficaces. Dans ce cas l'algorithme de segmentation par ligne des partage des eaux peut être utilisé de manière beaucoup plus efficace pour le marquage de grains ou de particules.
L'algorithme de segmentation est généralement utilisé pour la détection de minima locaux et pour la segmentation d'image en traitement d'image. Comme le problème de la détermination de la position des grains peut être considéré comme un problème de détection d'extrema locaux, cet algorithme peut être utilisé pour des besoins de segmentation ou de marquage de grains. Par souci de simplicité nous traiterons des données inversées selon la direction z pour la description de l'algorithme (c'est-à-dire que le sommet des grains sont des des minima locaux dans le texte qui suit). Deux niveaux de traitement sont appliqués pour l'analyse de grain (voir [1]) :
- Phase de localisation des grains : une goutte virtuelle est déposée en chaque point de la surface inversée (la quantité d'eau est contrôlée par le paramètre Taille de goutte). Dans le cas où la goutte ne se trouve pas déjà sur un minimum local, celle-ci suit la pente la plus forte afin de minimiser son énergie potentielle. La goutte s'arrête dès qu'elle atteind un minimum local. Elle remplit ainsi partiellement le minimum local en fonction de son volume (voir la figure et sa légende ci-dessous). Ce procédé est répété plusieurs fois (avec le paramètre Nombre de pas). Il en résulte un ensemble de lacs de différentes tailles remplissant la surface inversée. Les surfaces des lacs sont ensuite évaluées, et les plus petits d'entre eux sont supprimés, en prenant pour hypothèse que ceux-ci se sont formés dans les minima locaux provoqués par le bruit (tous les lacs plus petits que le paramètre Seuil sont supprimées). Les lacs les plus importants sont utilisés pour identifier la position des grains pour la segmentation lors de l'étape suivante. On élimine ainsi le bruit de mesure présent dans les données AFM.
-
Phase de segmentation : les grains trouvés lors de la première étape
sont marqués (chacun avec un numéro différent). Les gouttes continuent
de tomber vers la surface et de remplir les minima locaux (la quantité
d'eau est contrôlée par le paramètre Taille de goutte).
Le nombre total d'étapes d'aspersion de gouttes en chaque point de la
surface est contrôlé par le paramètre Nombre d'étapes.
Comme les grains ont déjà été marqués et identifiés lors de la première
étape, les situations suivantes peuvent apparaître dès qu'une goutte
atteind un minimum local :
- La goutte atteind un endroit déjà marqué comme étant un grain. Dans ce cas la goutte est fusionnée avec le grain, c'est-à-dire qu'elle est marquée comme faisant partie du même grain.
- La goutte atteind un endroit non marqué, mais un grain se trouve à proximité immédiate. Dans ce cas la goutte est là aussi fusionnée avec le grain.
- La goutte atteind un endroit non marqué et n'ayant aucun grain à proximité immédiate. Dans ce cas la goutte n'est pas marquée.
- La goutte atteind un endroit non marqué mais ayant plus d'un grain à proximité immédiate (par exemple lorsque deux grains se trouvent à proximité). Dans ce cas la goutte est marquée comme limite du grain.
- La goutte atteind un endroit marqué comme limite de grain. Dans ce cas la goutte est là aussi marquée comme limite de grain.
On peut ainsi identifier la position des grains et déterminer ensuite le volume occupé par chaque grain. On peut utiliser le paramètre Inverser les hauteurs dans le cas où les zones d'intérêt sont des vallées plutôt que des collines (grains)
→ →
Cette fonction est une approche différente basée sur l'algorithme de ligne de marquage des eaux, ici l'algorithme classique de Vincent de segmentation dans les espaces numériques [2], que l'on applique à une image pré-traitée. En général, le résultat est une image complètement segmentée en motifs, chaque pixel appartenant à un motif ou séparant deux d'entre eux. L'algorithme marque par défaut les vallées. Pour marquer les grains en reliefs, ce qui est le plus courant en microscopie, utilisez l'option inverser les hauteurs.
Le pré-traitement propose les paramètres suivants :
- Floutage gaussien
Dispersion du filtre gaussien appliqué aux données. Une valeur nulle indique qu'aucun filtrage n'est appliqué.
- Ajouter un gradient
Poids relatif du gradient local ajouté aux données. Une valeur importante signifie que les zones ayant une pente locale importante auront tendance à devenir des bords de grains.
- Ajouter de la courbure
Poids relatif de la courbure locale ajoutée aux données. Une valeur importante signifie que les zones localement concaves auront tendance à devenir des bords de grains.
- Niveau de barrière
Hauteur relative au-dessus de laquelle les pixels ne peuvent être assignés à des grains. Si elle diffère de 100 %, cela crée une exception à une segmentation complète de l'image.
- Niveau de pré-remplissage
Hauteur relative jusqu'à laquelle la surface est pré-remplie, supprimant tous les détails au fond des vallées.
- Pré-remplir à partir du minima
Hauteur relative jusqu'à laquelle la surface est pré-remplie à partir de chaque minimum local, supprimant tous les détails au fond des vallées.
→ →
On peut utiliser la régression logistique pour transférer une segmentation d'une image vers une autre ayant des motifs similaires, ou de petits morceaux d'image vers une image complète. Deux modes d'opération sont disponibles : l'apprentissage et l'application. La phase d'apprentissage nécessite la présence d'un masque des grains sur l'image. Lorsque la régression est calculée, elle peut être utilisée pour d'autres images. Dans les deux cas, elle génère un vecteur de motifs de l'image courante, et y applique différents filtres, parmi lesquels :
- Flou gaussien
Filtre gaussien de largeur 2, 4, 8, etc. Le nombre de gaussiennes peut être sélectionné à l'aide du sélecteur nombre de gaussiennes
- Dérivées de Sobel
Filtre de dérivation de Sobel pour les directions X et Y.
- Laplacien
Laplacien, somme des dérivées secondes.
- Hessienne
Trois éléments de la matrice hessienne des dérivées secondes, un pour chaque direction X et Y, et le troisième pour les coordonnées combinées.
Tous les filtres de dérivation, lorsqu'ils sont sélectionnés, sont appliqués à l'image originale ainsi qu'à chaque version filtrée par gaussienne, lorsqu'elles sont générées. Chaque couche de motifs est calculée par convolution puis normalisée.
Le paramètre de régularisation permet de régulariser la régression logistique, un valeur élevée signifie que les paramètres seront plus fortement contraints pour éviter des valeurs élevées.
Notez qu'il faut la présence d'un masque sur l'image pour l'apprentissage, dans le cas contraire le résultat sera nul. La phase d'apprentissage peut être très lente, en particulier pour les images de grande taille et lorsque de nombreux motifs sont sélectionnés. Les résultats de l'apprentissage sont sauvegardés, ils peuvent donc être appliqués à d'autres images. Si l'ensemble des motifs est modifié, il faudra à nouveau lancer l'apprentissage de la régression logistique.
Les propriétés des grains peuvent être analysées à l'aide de plusieurs fonctions. La plus simple d'entre elles est la Statistique des Grains
→ →
Cette fonction calcule le nombre de grains marqués, leur aire projetée, à la fois en valeur absolue et en fraction de l'aire totale du champ de données, le total des volumes des grains, la longueur totale des périmètres des grains, l'aire moyenne ainsi que la taille du carré équivalent des grains. La taille moyenne est calculée en moyennant la taille des carrés équivalents, donc le carré de cette moyenne n'est en général pas égal à l'aire moyenne.
Les caractéristiques globales de la zone marquée sont disponibles dans l'outil Statistiques en utilisant l'option Inclure uniquement la région masquée. On obtient les mêmes informations pour les zones non marquées en inversant le masque.
→ →
L'outil de calcul des distributions des grains est le plus puissant et le plus complexe. Il comporte deux modes d'opération : l'affichage de graphiques et l'export de données. Dans le mode affichage de graphiques, les caractéristiques sélectionnées sont calculées et rassemblées dans des graphes donnant leurs distributions.
L'export de données est utile pour les experts ayant besoin par exemple de corréler les propriétés des grains. Dans ce mode les caractéristiques sélectionnées sont calculées et compilées dans un fichier texte sous la forme d'un tableau où chaque ligne correspond à un grain et chaque colonne à une caractéristique. L'ordre des colonnes est identique à celui des quantités présentées dans la fenêtre de dialogue ; toutes les valeurs sont données en unités SI, comme partout dans Gwyddion.
→ →
Affiche un graphe de corrélation d'une caractéristique en fonction d'une autre, permettant ainsi de visualiser les corrélations entre celles-ci.
L'outil de mesure des grains est une manière interactive de déterminer les mêmes caractéristiques que celles données par distribution des grains en mode texte. Il suffit de cliquer sur un grain dans la fenêtre de données pour que toutes les quantités soient affichées dans la fenêtre de l'outil.
Cet outil affiche aussi le numéro du grain. Le numéro du grain correspond au numéro de ligne (en partant de 1) des fichiers exportés par le calcul des distributions des grains.
Les distribution des grains et l'outil de mesure des grains peuvent alculer les caractéristiques suivantes :
- Caractéristiques liées à la valeur
- Minimum, valeur (hauteur) minimale présente dans le grain.
- Maximum, valeur (hauteur) maximale présente dans le grain.
- Moyenne, moyenne des valeurs présentes dans le grain, c'est-à-dire la hauteur moyenne du grain.
- Médiane médiane des valeurs présentes dans le grain, c'est-à-dire la hauteur médiane du grain.
- Minimum du bord, valeur (hauteur) minimale présente sur le bord interne d'un grain. Le bord est représenté par les pixels présents dans le grain et ayant au moins un pixel voisin en dehors du grain.
- Maximum du bord, valeur (hauteur) maximale présente sur le bord interne d'un grain, défini de la même manière que pour le minimum.
- Caractéristiques liées à la surface
- Surface projetée, aire projetée (c'est-à-dire plane) du grain.
- Côté équivalent, taille du carré ayant la même surface que la surface projetée du grain.
- Rayon équivalent, rayon du disque ayant la même surface que la surface projetée du grain.
- Surface, surface du grain, reportez-vous à la section quantités statistiques pour une description de la méthode d'estimation de la surface.
- Aire de l'enveloppe convexe, aire projetée de l'enveloppe convexe du grain. Celle-ci est légèrement plus grande que la surface du grain, même pour les grains visiblement convexe, à cause de la pixellisation du masque. Seuls les grains parfaitement rectangulaires ont la même surface.
- Caractéristiques liées au bord
- Périmètre projeté, longueur du bord du grain projeté sur le plan horizontal (et non sur la surface tri-dimensionnelle). La méthode d'estimation du périmètre est décrite plus bas.
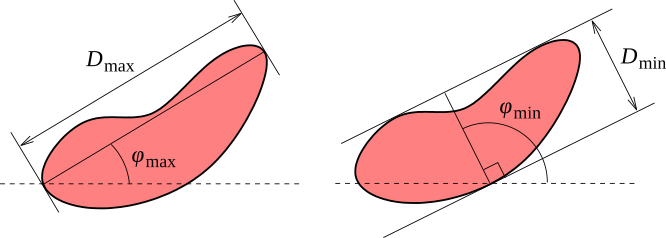
- Largeur, dimension minimale du grain dans le plan horizontal. On peut voir celle-ci comme étant le plus petit écart au travers duquel passerait le grain.
- Orientation de la largeur, orientation de l'écart décrit précédemment. Si le grain présente une symétrie lui conférant plusieurs directions possibles, celle-ci est choisie arbitrairement.
- Longueur, dimension maximale du grain dans le plan horizontal. On peut voir celle-ci comme étant le plus grand écart que le grain pourrait remplir
- Orientation de la longueur, orientation de l'écart décrit précédemment. Si le grain présente une symétrie lui conférant plusieurs directions possibles, celle-ci est choisie arbitrairement.
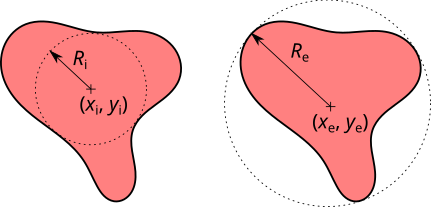
- Rayon maximal du disque inscrit, rayon du disque le plus grand pouvant s'inscrire dans le grain. Le disque entier doit s'incrire, pas seulement le cercle extérieur, ce qui a son importance dans le cas des grains présentant des vides. Vous pouvez utiliser l'éditeur de masque pour remplir les vides présents dans les grains.
- Position x du centre du disque inscrit maximal, coordonnée horizontale du centre du disque inscrit maximal. Plus précisément, une des coordonnées si le disque n'est pas unique.
- Position y du centre du disque inscrit maximal, coordonnée verticale du centre du disque inscrit maximal. Plus précisément, une des coordonnées si le disque n'est pas unique, mais elle correspond au même disque que celui de la donnée précédente.
- Rayon minimal du disque circonscrit, rayon du plus petit cercle pouvant contenir le grain.
- Position x du centre du disque circonscrit, coordonnée horizontale du centre du cercle circonscrit.
- Position y du centre du disque circonscrit, coordonnée horizontale du centre du cercle circonscrit.
- Rayon moyen, distance moyenne entre le barycentre du grain et le bord de celui-ci. Cette quantité n'est en général utile que dans le cas des grains convexes ou quasi-convexes.
- Caractéristiques liées au volume
- Base zéro, volume entre la surface du grain et le plan z = 0. Les valeurs en-dessous de zéro représentent un volume négatif. Le niveau zéro doit être défini à une valeur raisonnable (en général la fonction fixer le zéro suffit) pour que le résultat ait un sens, ce qui est aussi l'avantage de cette méthode : on peut utiliser le plan de base que l'on souhaite.
- Base minimum du grain, volume entre la surface du grain et le plan z = zmin, où zmin est la valeur (hauteur) minimale présente dans le grain. Cette méthode tient compte de l'environnement du grain, mais typiquement elle sous-estime le volume, en particulier pour les petits grains.
- Base arrière-plan laplacien, volume entre la surface du grain et la surface de base formée par l'interpolation laplacienne des valeurs environnantes. Plus précisément, il s'agit du volume qui disparaîtrait après avoir appliquéla fonction supprimer les données sous le masque ou l'outil suppression de grain avec l'interpolation laplacienne. Il s'agit de la méthode la plus sophistiquée, mais aussi la moins intuitive.
- Caractéristiques liées à la position
- Position centrale x, coordonnée horizontale du centre du grain. Comme la surface du grain est définie par la surface couverte par les pixels du masque, le centre d'un grain ne faisant qu'un seul pixel sera un demi-entier et non un entier. Le décalage de l'origine du champ de données est pris en compte.
- Position centrale y, coordonnée horizontale du centre du grain. Voir l'interprétation plus haut.
- Caractéristiques liées à la pente
- Inclinaison θ, déviation de la normale du plan moyen par rapport à l'axe z, reportez-vous au paragraphe inclinaisons pour plus de détails.
- Inclinaison φ, azimuth de la pente, telle que définie dans le paragraphe inclinaisons.
- Caractéristiques liées à la courbure
- Position x du centre de courbure, position horizontale du centre de la surface quadratique ajustée à la surface du grain.
- Position y du centre de courbure, position verticale du centre de la surface quadratique ajustée à la surface du grain.
- Valeur z du centre de courbure, valeur au centre de la surface quadratique ajustée à la surface du grain. Notez qu'il s'agit de la valeur sur la surface ajustée et non sur la surface réelle.
- Courbure 1, la plus petite courbure (c'est-à-dire l'inverse du rayon de courbure) au centre.
- Courbure 2, la plus grande courbure (c'est-à-dire l'inverse du rayon de courbure) au centre.
- Angle de courbure 1, direction correspondant à Courbure 1.
- Angle de courbure 2, direction correspondant à Courbure 2.
- Caractéristiques liées au moment
- Demi-grand axe de l'ellipse équivalente, longueur du demi-grand axe de l'ellipse ayant les mêmes moments d'ordre deux dans le plan horizontal.
- Demi-petit axe de l'ellipse équivalente, longueur du demi-petit axe de l'ellipse ayant les mêmes moments d'ordre deux dans le plan horizontal.
- Orientation de l'ellipse équivalente, direction du demi-grand axe de l'ellipse ayant les mêmes moments d'ordre deux dans le plan horizontal. L'angle vaut par définition zéro pour un grain circulaire.
Le périmètre des grains est estimé en sommant des contributions estimées de chacune des configurations à quatre pixels sur le bord du grain. Les contributions sont affichées sur la figure suivante pour chaque configuration, où hx et hy sont les dimensions du pixel selon les axes correspondants, et h est la longueur de la diagonale du pixel :
Les contributions correspondent une à une aux longueurs des segments du bord du polygone approximant la forme du grain. La construction du polygone équivalent est aussi visible sur la figure.
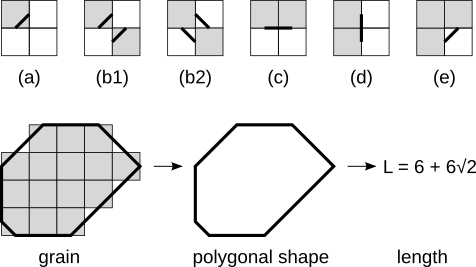
Contributions des configurations de pixels sur la longueur estimée du bord (en haut). Les carrés en gris représentent les pixels à l'intérieur du grain, et les carrés en blanc ceux à l'extérieur. La contribution estimée de chaque configuration est : (a) h/2, (b1), (b2) h, (c) hy, (d) hx, (e) h/2. Les cas (b1) et (b2) ne diffèrent que dans la visualisation de la forme des segments du polygone, les longueurs estimées du bord sont identiques. La partie inférieure de la figure illustre la manière dont les segments se joignent pour former le polygone.
Le volume est, après soustraction de la base, estimée comme étant le volume de l'objet dont la surface supérieure est celle utilisée pour le calcul de surface. Notez que pour le volume entre les vertex, ceci est équivalent à la méthode classique des trapèzes pour l'intégration en deux dimensions. Cependant, nous calculons le volume sous un masque centré sur les vertex, leur contribution à l'intégrale est donc distribuée de manière différente, tel que montré dans la figure suivante.
Les caractéristiques liées à la courbure des grains sont calculées de manière identique à la courbure globale donnée par la fonction courbure. Référez-vous à sa description pour plus de détails.
Les disques inscrits et les cercles circonscrits aux grains peuvent être visualisés en utilisant → → et → → . Ces fonctions créent des sélections circulaires représentant les disques et cercles correspondants pour chaque grain, celles-ci pouvant être affichées par la suite avec le gestionnaire de sélections.
Les grains marqués peuvent être filtrés par seuillage sur différentes quantités à l'aide de la fonction → → . Ce module peut être utilisé pour des opérations basiques, telle que la suppression de petits grains à l'aide d'un seuillage basé sur l'aire, ou des filtrages bien plus complexes à l'aide d'expressions logiques impliquant différentes quantités.
Le filtre conserve les grains satisfaisant les conditions définies dans
Conserver les grains satisfaisant et supprime tous
les autres. La condition est exprimée par l'association logique de une à
trois conditions, notées A, B et
C. L'expression la plus simple est juste
A, qui impose que la quantité A
soit entre les seuils définis.
Chaque condition consiste en deux seuils haut et bas pour une quantité donnée, par exemple l'aire ou la valeur minimale. Les valeurs doivent appartenir à l'intervalle [bas,haut] pour satisfaire la condition et conserver ainsi les grains. Notez qu'il est possible de choisir un seuil bas plus élevé que le seuil haut. Dans ce cas la condition est inversée, c'est-à-dire que le grain est conservé si la valeur est en dehors de l'intervalle [haut,bas].
Les quantités sont assignées à A,
B et C en sélectionnant la quantité
dans la liste puis en cliquant sur le bouton correspondant dans
Assigner à. L'ensemble des quantités sélectionnées
est affiché dans les en-têtes
Condition A,
Condition B et
Condition C.
Les grains peuvent être alignés verticalement en utilisant → → . Cette fonction décale verticalement chaque grain de façon à ce qu'une caractéristique liée à la hauteur soit égale pour tous les grains. En général, on aligne la valeur minimale des grains, mais d'autres choix sont possibles.
Les données entre les grains sont aussi décalées verticalement. Les décalages sont interpolés par rapport aus décalages des grains à l'aide de l'équation de Laplace, ce qui donne une transition douce des décalages entre les grains (toutefois on ne considère pas les autres éléments présents sur la surface).
[1] Petr Klapetek, Ivan Ohlídal, Daniel Franta, Alberto Montaigne-Ramil, Alberta Bonanni, David Stifter and Helmut Sitter: Acta Physica Slovaca, 3 (223-230) 2003
[2] Luc Vincent and Pierre Soille: IEEE Transactions on Pattern Analysis and Machine Intelligence, 13 (583–598) 1991