Помимо функций для анализа измеренных данных Gwyddion предлагает несколько генераторов искусственных поверхностей которые можно также использовать для тестирования или моделирования вне Gwyddion [1].
Все генераторы поверхностей имеют некоторый общий набор параметров, определяющих размеры и масштабы созданной поверхности и элементов управления генератором случайных чисел. Эти параметры описаны ниже, параметры, специфичные для каждого генератора описаны в соответствующих подразделах.
Параметры изображения:
- Горизонтальный, вертикальный размер
Горизонтальное и вертикальное разрешение создаваемой поверхности в пикселях.
- Квадратное изображение
Включение этой опции делает горизонтальное и вертикальное разрешения одинаковыми.
- Ширина, высота
Горизонтальные и вертикальные физические размеры создаваемой поверхности в выбранных единицах. Следует отметить, что квадратные пиксели считаются таковыми, изменение одного параметра ведёт к изменению другого.
- Единицы измерения пространства и значений
Единицы измерения пространственных размеров (Ширина, Высота) и значений (высот). Выбранные здесь единицы измерения также определяют единицы измерения не безразмерных параметров отдельных генераторов.
Нажатие этой кнопки приводит к заполнению всех вышеперечисленных параметров в соответствии с текущим изображением.
Следует отметить, что хотя единицы измерения значений обновляются, масштаб значений определяется зависящими от генератора параметрами, которые могут не выводиться напрямую из статистических свойств текущего изображения. Следовательно, эти параметры не пересчитываются.
- Заменить текущее изображение
Эта опция имеет двойной эффект. Во первых, она заставляет размеры и масштабы автоматически устанавливаться равными текущему изображению. Во вторых, при этом генерируемая поверхность заменяет текущее изображение вместо создания нового.
- Начать с текущего изображения
Эта опция имеет двойной эффект. Во первых, она заставляет размеры и масштабы автоматически устанавливаться равными текущему активному изображению. Во вторых, она заставляет генератор начать с поверхности, содержащейся в текущем изображении и модифицировать её вместо плоской поверхности. Следует отметить, что это не влияет на то, будет ли результат записан в текущее изображение или будет создано новое.
Элементы управления генератором случайных чисел:
- Случайное зерно
Начальное число генератора случайных чисел. При выборе тех же параметров и разрешений и того же начального числа генерируется та же самая поверхность, даже на разных компьютерах. Различные начальные числа приводят к генерации разных поверхностей с теми же общими характеристиками, заданными параметрами генератора.
Заменяет начальное число случайным.
- Сделать случайным
Включение этой опции приводит к тому, что начальное число выбирается случайно при каждом запуске генератора. Это позволяет удобно перезапускать генератор просто нажимая Ctrl-F (см. раздел клавиатурные сокращения).
Обновить/просмотреть элементы управления:
- Обновлять сразу
Если этот флаг включен, поверхность рассчитывается заново после каждого изменения входных параметров. Эта опция доступна для генераторов которые работают относительно быстро.
- Прогрессивное обновление
Если этот флаг включен, изображение предпросмотра показывает развитие морфологии поверхности в процессе симуляции. Эта опция доступна для медленных генераторов, которые задействуют итерационные физические модели. Включение прогрессивного обновления в общем случае слегка замедляет симуляцию, поскольку снимки требуют некоторого времени для своего получения и отображения.
Модуль спектрального синтеза создаёт случайно шероховатые поверхности путём синтеза преобразования Фурье поверхности в соответствии с заданными параметрами и затем применением обратного преобразования Фурье для получения реальной поверхности. Генерируемые поверхности являются периодическими (т.е. идеально гладко сшиваются на границах).
Параметры Фурье-образа определяют форму функции спектральной плотности мощности, т.е. модулей коэффициентов Фурье, фазы задаются случайно. В настоящий момент все создаваемые поверхности изотропны, т.е. функция спектральной плотности мощности радиально симметрична.
- Ср. квадр.
Среднеквадратичное значение высот (или отличий от средней плоскости, которая, однако, всегда является плоскостью z = 0). Кнопка как у текущего изображения устанавливает значение среднеквадратичного отклонения равным таковому для текущего изображения.
- Минимальная, максимальная частота
Минимальная и максимальная пространственные частоты. Увеличение минимальной частоты ведёт к «уплощению» изображения, т.е. удалению крупных выделяющихся частей. Уменьшение максимальной частоты ограничивает остроту выступающих частей.
- Разрешить гауссов множитель
Включает умножение коэффициентов Фурье на гауссову функцию, что в реальном пространстве соответствует свёртке с гауссианой.
- Разрешить лоренцев множитель
Включает умножение коэффициентов в разложении Фурье на функцию, пропорциональную 1/(1 + k2T2)3/4, где T — длина автокорреляции. Таким образом, сам множитель фактически не является лоренцевым, но он соответствует лоренцевой одномерной плотности спектра мощности, которая в свою очередь соответствует экспоненциальной функции автокорреляции (подробное обсуждение функций автокорреляции приведено в разделе Статистический анализ). Этот множитель убывает сравнительно медленно, таким образом, ограниченное разрешение играет обычно большую роль, чем в случае с гауссовым.
- Длина автокорреляции
Длина автокорреляции гауссова или лоренцева множителя (подробное обсуждение функций автокорреляции приведено в разделе Статистический анализ).
- Разрешить степенной множитель
Включает умножение коэффициентов в разложении Фурье на множитель, пропорциональный 1/kp, где k - пространственная частота и p - степень. Это позволяет создавать различные фрактальные поверхности.
- Степень
Степень p.
Метод размещения объектов позволяет создавать случайные поверхности, состоящие из выступающих частей определённой формы. Алгоритм прост: заданное число объектов помещается в случайные места поверхности. Для каждого из размещаемых объектов, новые высоты меняются на max(z, z0 + h), где z – текущая высота отдельной точки, h – высота объекта в этой точке (подразумевая нулевой базис) и z0 – текущая минимальная высота над базисом помещаемого объекта. Алгоритм рассматривает горизонтальную плоскость как заполненную идентичными копиями поверхности, следовательно, и сама поверхность будет периодически повторяющейся (т.е. будет идеально совмещаться сама с собой на границах при использовании в качестве текстуры).
|

|

|

|
| Пирамида | Бриллиант | Тетраэдр | Гексагональная пирамида |

|

|

|

|
| Конус | Полусфера | Половина сварной точки | Параболический выступ |

|

|

|

|
| Гауссиана | Экспоненциальный выброс | Полная сфера | Сварная точка |
|

|

|

|
| Параллелепипед | Камыш | Полупирамида | Палатка |

| |||
| Бублик |
Параметры и настройки на вкладке Форма управляют формой отдельных особенностей:
- Форма
Форма (тип) размещаемых объектов. В настоящее время возможные варианты включают: полусферы, прямоугольные параллелепипеды, различные пирамиды, бугры, иглы и некоторое количество более странных форм. Разница между полусферой и полной сферой состоит в высоте. Полная сфера включает также высоту нижней половины. То же самое относится и к сварным точкам.
- Размер
Пространственный размер объекта, обычно сторона описанного квадрата.
- Пропорции
Соотношение между размерами по x и y объекта по отношению к некоторым пропорциям по умолчанию.
Изменение соотношения сторон не всегда подразумевает простое геометрическое масштабирование, например, объекты, называемые частицами меняют форму от полусфер до стержней при изменении соотношения сторон.
- Высота
Величина, пропорциональная высоте объекта, обычно высота самой высокой точки.
Включение опции Масштабируется с размером заставляет невозмущенные высоты масштабироваться пропорционально размерам отдельных объектов. В противном случае высота не зависит от размера. Пропорциональное масштабирование полезно при использовании ненулевого разброса размеров чтобы сохранить форму всех объектов одинаковой (в противоположность их вертикальному удлинению и уплощению). Если все объекты имеют одинаковый размер, опция никак не влияет на результат.
Кнопка как у текущего изображения устанавливает значение высоты равным значению, основанном на среднеквадратичном отклонении текущего изображения.
- Усечение
Фигуры могут быть усечены на определённой высоте для создания усечённых конусов, пирамид, и т.п. Высота усечения задаётся в долях от общей высоты объекта. Единица означает неусечённую фигуру, ноль – полное удаление объекта.
Каждый параметр может быть задан случайно для отдельных объектов, это задаётся опцией Разброс. Для мультипликативных величин (все, кроме ориентации и усечения), распределение логарифмически нормальное со значением среднеквадратичного отклонения логарифма величины заданным параметром Разброс.
Параметры и настройки на вкладке Размещение управляют где и как поверхность будет меняться с помощью сгенерированных фигур:
- Покрытие
Среднее количество раз, которое объект перекрывает пиксель изображения. Значение покрытия 1 означает что поверхность будет ровно один раз покрыта объектами, при этом они будут покрывать её равномерно. Большие значения означают больше слоёв объектов и более медленную генерацию изображения.
- Направление особенности
Направление изменения поверхности при добавлении объектов. Положительные и отрицательные изменения соответствуют образованию высот и впадин при добавлении объектов соответственно. Нулевое значение параметра означает что выступы и впадины выбираются случайно. Положительное значение делает выступы более вероятными, максимальное значение, равное 1 соответствует формированию только выступов. То же самое справедливо для отрицательных значений и впадин.
- Рост плёнки колоннами
Для столбчатости равной нулю локальная модификация поверхности работает как описано во введении. Для столбчатости равной одному (максимальной) объекты считаются имеющими также нижнюю часть, которая является идеальным зеркальным отражением (видимой) верхней части. Как только нижняя часть касается любой точки поверхности, она прилипает к ней. Это задаёт итоговую высоту. Диапазон высот растёт быстро в данном случае и объём будет достаточно пористым (что не представлено полем высот, разумеется). Значения между 0 и 1 означают что высота объекта интерполируется между двумя экстремумами.
- Избегать наложения
Если эта опция включена, на любой пиксель поверхности может быть помещено не более одного объекта. Следовательно, они никогда не будут пересекаться. Опция Покрытие в данном случае не задаёт сколько объектов будет реально помещено на поверхность, а только количество попыток генератора разместить объект. Как только не остаётся свободного места, куда можно поместить объект заданного размера, увеличение покрытия не будет влиять на результат (только замедлять генерацию).
- Ориентация
Поворот решетки по отношению к определённому исходному направлению, измеренный против часовой стрелки. Ориентация также может быть сделана случайной используя соответствующую настройку Разброса.
Осаждение частиц проводит динамическое моделирование падения взаимодействующих сферических частиц на твёрдую поверхность. Частицы не падают все одновременно. Вместо этого, они падают последовательно между частицами уже лежащими на поверхности и им даётся время для релаксации.
- Радиус частицы
Радиус сферических частиц в физических единицах. Высота и пространственные размеры должны быть одной и той же физической величиной, следовательно, тут будет только один параметр размерности.
- Ширина распределения
Стандартное отклонение распределения радиуса (гауссова).
- Покрытие
Какая часть поверхности должна быть покрыта, если она равномерно покрывается осаждаемыми частицами. если модель не может разместить требуемого числа частиц, обычно вследствие слишком малого времени симуляции, выводится сообщение об ошибке.
- Шагов релаксации
Длина моделирования, измеренная в количестве шагов.
Метод осаждения стержней основан на том же динамическом моделировании, но для продолговатых частиц. Частицы в действительности формируются триплетами сфер, тем не менее, это позволяет получить достаточно вменяемый диапазон соотношений размеров частиц. Модель также имеет несколько дополнительных параметров взаимодействия.
Генератор искусственных поверхностей Объекты достаточно быстр, но это достигается избеганием любых видов трёхмерной геометрии и только тем, что поверхность изменяется по простым правилам. Модули осаждения частиц и стержней лежат около другого конца спектра скорость-реализм и действительно выполняют динамическое моделирование падения на поверхность взаимодействующих частиц. Этот модуль лежит посередине, поскольку он формирует поверхность из реальных трёхмерных твёрдых объектов, но по прежнему использует только простые правила для того, что происходит с ними когда они касаются поверхности, сохраняя хорошую скорость генерации поверхности.
Объекты начинают падать из горизонтального положения. Когда они касаются поверхности, находится положение локальной средней плоскости вокруг области контакта. Фигура после этого поворачивается так, чтобы лежать прямо на этой локальной плоскости, её финальная высота определяется как подробнее описано в описании Столбчатости ниже, и затем она просто прилипает в этом положении. Дальнейшее соскальзывание, кувыркание, обрушение и прочие динамические усадочные процессы не моделируются.
Некоторые параметры генератора имеют точно такое же значение, что и для синтеза Объектов. Это включает в себя Покрытие, Избегать наложения и Ориентация. Остальные описаны ниже:
- Форма
Форма (вид) помещаемых объектов. В настоящее время возможные варианты включают в себя различные удлинённые формы.
- Ширина
Формы могут быть вытянуты вдоль оси x (что контролируется опцией Соотношение сторон). Их размер в перпендикулярном направлении задаётся шириной. Поперечное сечение будет симметричным. Следовательно, ширина задаёт сразу и горизонтальную ширину, и высоту.
- Соотношение сторон
Отношение между размерами вдоль направлений x и y. Другими словами, вытянутость. Оно всегда не меньше единицы, формы никогда не сжимаются вдоль оси x. Следовательно, распределение соотношения размеров может быть сильно асимметричным, если номинальное значение близко к единице и разброс велик.
- Рост плёнки колоннами
В общем случае, этот параметр влияет на то, насколько фигуры склонны образовывать колоннообразные структуры (пористые, если топографические данные могут это представить). Значение по умолчанию, равное нулю, можно представить как если бы нижняя часть фигуры плавилась при взаимодействии и заполняла впадину, куда она упала. Следует отметить, что объёмное равновесие является в какой-то мере приблизительным и высота, на которой застревает объект может быть такой, что острые выступы на поверхности пробивают его насквозь.
Максимальная столбчатость (1) означает, что как только любая часть формы касается поверхности, она прилипает к ней. Для меньших положительных значений финальная высота интерполируется парой высот, заданной двумя подходами.
Если столбчатость отрицательна, форма вбита в поверхность. Для минимального значения (-1) оно опускается на наименьшую высоту, для которой по крайней мере одна точка всей её нижней границы не будет ниже оригинальной поверхности. Снова, для других отрицательных значений финальная высота будет интерполирована.
Случайный некоррелированный точечный шум генерируется независимо в каждой точке. Доступно несколько распределений.
- Распределение
Распределение значения шума. Варианты включают в себя гауссово, экспоненциальное, равномерное и треугольное распределения, распределение вида соль и перец.
Распределение вида соль и перец работает несколько отлично от того, которое является привычным для работающих с компьютерной графикой, поскольку диапазон значений неограничен. Это бимодальное распределение состоящее из двух δ-функций. Другими словами, константа (задаваемая с помощью RMS) добавляется и/или вычитается из каждого значения пикселя.
- Направление
Шум можно генерировать как симметричный, так и односторонний. Среднее значение распределения симметричного шума равно нулю, т.е. среднее значение данных не меняется при добавлении симметричного шума. Односторонний шум только увеличивает (положительный) или уменьшает (отрицательный) значения данных.
- Ср. квадр.
Среднеквадратичное значение распределения шума. Точнее, среднеквадратичное соответствующего симметричного распределения в случае одностороннего шума.
- Плотность
Плотность показывает долю значений, которые будут изменяться. Если она равна 1, то изменятся все пиксели изображения. Если она меньше, некоторые останутся неизменными.
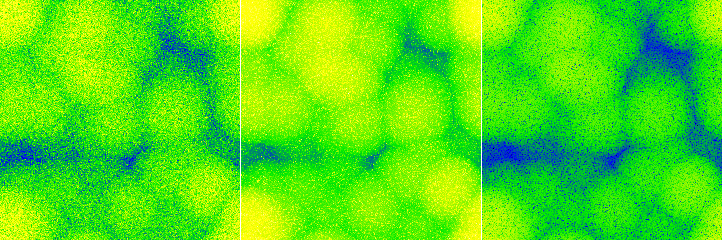
Различные виды искусственного шума, добавленные к одной и той же поверхности: симметричный гауссов шум (слева), положительный экспоненциальный шум (по центру), отрицательный экспоненциальный шум (справа). Все изображения показаны с одинаковой шкалой псевдоцвета и все виды шума имеют одинаковое среднеквадратичное отклонение.
Линейный шум представляет собой шум с длительностью больше пренебрежимо малой, который приводит к типичным ступеням или царапинам (они же называются штрихами) в направлении быстрой оси сканирования или смещенным линиям сканирования. Параметры Распределение, Направление и Среднеквадратичное отклонение имеют те же значения, что и для точечного шума. Другие параметры управляют пространственными характеристиками шума.
Доступны следующие основные типы линейных дефектов:
- Ступеньки представляет собой резкое изменение значений которое продолжается до конца скана (или до возникновения следующей ступени).
- Царапины это локальные изменения значения с конечной длиной, т.е. значения возвращаются к оригинальному уровню в пределах той же линии скана.
- Борозды подобны царапинам, но на большем масштабе: они могут продолжаться на несколько линий сканирования.
- Наклон создает разброс наклонов отдельных линий сканирования, в противоположность тому, чтобы напрямую сдвигать их высоту.
- Автогенерация (жужжание) добавляет квазипериодическое возмущение, моделирующее тип шума возникающий из электронных помех.
Ступеньки имеют следующие параметры:
- Плотность
Среднее число дефектов на линию скана, включая любое время простоя (которое определяется параметром Рабочий ход).
- В пределах линии
Доля времени сканирования линии, которая тратится непосредственно на снятие данных. Остальное время относится к холостому ходу. Значение 1 соответствует случаю нулевого времени холостого хода, т.е. все ступени появляются в пределах изображения. Значение 0 означает, что время снятия данных пренебрежимо мало к общему времени сканирования линии, следовательно, ступени могут встречаться только между линиями.
- Направление сканирования
Если ступени могут возникать внутри линии сканирования это задаёт горизонтальное направление сканирования (предполагается что медленная ось сканирования направлена сверху вниз). Для сканирования слева направо левая часть линии сканирования будет непрерывна с данными выше и нижняя с данными ниже. Для сканирования справа налево наоборот. Два направления проиллюстрированы в описании Блочной коррекции ступеней, которая исправляет подобные артефакты.
- Кумулятивные
Для кумулятивных ступеней случайное значение всегда добавляется к текущему значению данных; для одиночных ступеней новое смещение данных напрямую равно случайному значению смещения.
Для царапин доступны следующие параметры:
- Покрытие
Доля изображения покрытая дефектами, если они не пересекаются. Поскольку дефекты могут пересекаться, значение покрытия 1.0 не означает, что изображение полностью закрыто объектами.
- Длина
Длина царапины в пикселях.
- Разброс
Разброс длины царапины, описание в разделе объекты.
Гребни имеют следующие параметры:
- Плотность
Среднее число дефектов на линию скана, включая любое время простоя (которое определяется параметром Рабочий ход).
- В пределах линии
Доля времени сканирования линии, которая тратится непосредственно на снятие данных. Остальное время относится к холостому ходу. Значение 1 соответствует случаю нулевого времени холостого хода, т.е. все ступени появляются в пределах изображения. Значение 0 означает, что время снятия данных пренебрежимо мало к общему времени сканирования линии, следовательно, ступени могут встречаться только между линиями.
- Направление сканирования
Если ступени могут возникать внутри линии сканирования это задаёт горизонтальное направление сканирования (предполагается что медленная ось сканирования направлена сверху вниз). Для сканирования слева направо левая часть линии сканирования будет непрерывна с данными выше и нижняя с данными ниже. Для сканирования справа налево наоборот. Два направления проиллюстрированы в описании Блочной коррекции ступеней, которая исправляет подобные артефакты.
- Ширина
Средняя длина дефекта, измеренная в единицах размера изображения. Значение 1 означает что средней длиной будет всё время сканирования изображения. Малые значения означают что дефекты в основном будут занимать только одну линию сканирования.
Наклон имеет следующие параметры:
- Разброс смещений
С нулевым смещением все линии сканирования наклонены относительно середины. Другими словами, центральный столбец изображения не искажается. Увеличение разброса смещений случайно сдвигает точки поворота больше и больше влево и вправо от центра.
Гудение имеет следующие параметры:
- Длина волны
Характеристическая частота жужжания, измеренная в размерах изображения.
- Разброс
Малый разброс означает что шум будет очень узкополосным и будет выглядеть более-менее похоже на чистую синусоидальную волну. Большие значения порождают более широкий спектр с биениями и более искаженным профилем.
- Компоненты
Число случайных синусоидальных компонент, которые будут использованы чтобы сконструировать шум в каждой линии сканирования.
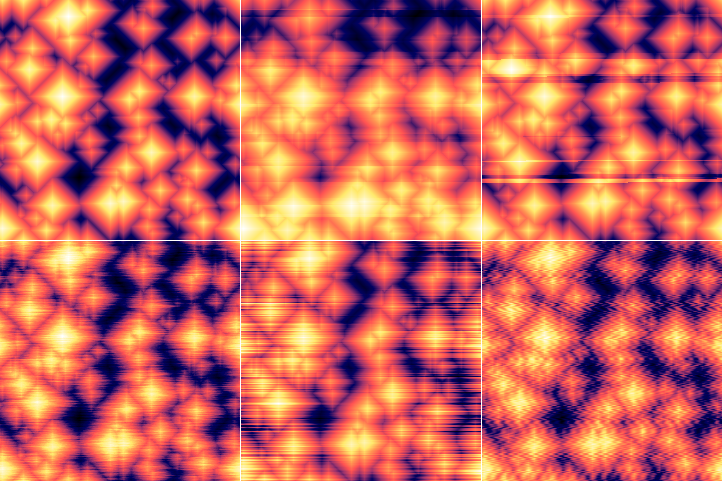
Различные виды линейного шума добавленные к искусственной пирамидальной поверхности: Верхний ряд: исходная поверхность (слева); относительно редкие кумулятивные ступени (по центру); относительно редкие борозды (справа). Нижний ряд: царапины со средней длиной 16 пикселей и высокой степенью покрытия (слева); наклон с малым разбросом смещений (по центру); автогенерация с настройками по умолчанию (справа).
Правильные геометрические текстуры, представляют поверхности, часто встречающиеся в микроскопии в качестве стандартов или тестовых образцов. В настоящее время может генерировать следующие типы текстур:
- Лестница
Одномерную лестничную текстуру, сформированную ступенями постоянной ширины и высоты.
- Решетка
Одномерная текстура, сформированная двусторонними ступенями (гребнями) постоянной ширины и высоты.
- Амфитеатр
Текстура в виде суперэллипса, сформированная ступенями постоянной ширины и высоты.
- Концентрические круги
Текстура в виде суперэллипса, сформированная двусторонними ступенями (гребнями) постоянной ширины и высоты.
- Звезда Сименса
Круговая текстура, сформированная сменяющими друг друга высокой и низкой кромками.
- Отверстия (прямоугольные)
Двумерная регулярная структура из прямоугольных отверстий, возможно квадратных.
- Колонны
Двумерная правильная упорядоченная структура симметричных колонн нескольких возможных видов (круглых, квадратных или шестигранных).
- Двойная лестница
Двумерная регулярная структура из ступеней фиксированной ширины и высоты.
Каждый тип текстуры имеет свой набор геометрических параметров, задающих форму и размер различных частей текстуры. Они описаны в следующих разделах. Большая часть геометрических параметров имеет также связанное с ними управление разбросом, подобное используемому в синтезе объектов, что позволяет сделать некоторые аспекты текстуры менее упорядоченными.
Расположение структуры на горизонтальной поверхности управляется параметрами на вкладке Положение, общей для всех видов шаблонов:
- Ориентация
Поворот текстуры по отношению к определённому исходному направлению, измеренный против часовой стрелки.
Эта вкладка также содержит параметры деформации. Включение разброса параметров делает поверхность в какой-то степени неправильной, однако, форма характерных особенностей поддерживается неизменной. Это дополняется другим методом изменения, называемым Деформация который разрешает искажение шаблона в плоскости xy. У деформации есть два параметра:
- Амплитуда
Величина пространственной деформации. Относительная численная величина в основном определяющая как далеко может зайти деформация.
- Пространственный масштаб
Характерный размер деформаций. Он описывает не как далеко смещаются характерные части изображения, а как резко или медленно сама деформация меняется вдоль горизонтальной плоскости.
Деформация работает аналогично двумерной гауссовой деформации, применяемой с помощью поля смещения. Однако, в данном случае она применяется к координатной системе перед тем, как отрисовывать текстуру, в то время, как поле смещения искажает уже дискретизированные изображения.
Все текстуры также имеют параметр Высота, задающий высоту элементов текстуры в физических единицах измерения. Для текстур по типу лестницы, которые растут непрерывно этот параметр задаёт высоту одной ступени. Для текстур, состоящих из выступов или впадин относительно ровной базовой плоскости этот параметр задаёт высоту одного отдельного элемента (если она не модифицирована Разбросом).

Поверхности на основе искусственных текстур. Верхний ряд: острые ступени, деформированные с большой длиной волны, масштабированная решетка с большим разбросом ширины и широкими асимметричными уклонами, слегка деформированный амфитеатр с отрицательной параболичностью, и концентрические круги с положительной параболичностью и меняющейся высотой. Нижний ряд: звезда Сименса с увеличенной верхней гранью, длинные прямоугольные отверстия с меняющимся вертикальным размером и положением, ряды слегка деформированных круглых колонн и двойная лестница с меняющейся шириной ступени.
Лестница имеет следующие особые параметры:
- Ширина террасы
Ширина одной ступени, заданная в пикселях, но также отображаемая в физических единицах. Все остальные размеры в горизонтальной плоскости задаются как доля этой базовой ширины.
Ширина включает в себя ширину наклонной части и может рассматриваться как «период» текстуры.
- Разброс положения
Случайное положение кромки ступени. Кромки никогда не пересекаются. Даже для максимального уровня случайности, они могут максимум коснуться края следующей ступени.
- Ширина уклона
Доля ширины, занятая наклонной кромкой. нуль означает острые ступени, единица означает, что текстура будет ровным уклоном (без рандомизации или влияния других модифицирующих параметров).
- Масштабируется с длиной
Если включено для высоты ступени, высота будет настраиваться чтобы быть пропорциональной ширине окружающих террас, при этом сохраняя среднюю высоту ступеней заданной. Этот подход наиболее близко сохраняет среднюю плоскость поверхности даже для случайной ширины ступеней.
Решетка имеет следующие особые параметры:
- Период
Период текстуры, заданный в пикселях, но также отображаемый в физических единицах. Все остальные размеры в горизонтальной плоскости задаются как доля этой базовой ширины.
- Разброс положения
Рандомизация ширины отдельных пар гребень-желоб.
- Масштабировать особенности с шириной
Если включено, то все горизонтальные размеры масштабируются пропорционально ширине каждой отдельной пары гребень-впадина для рандомизированных текстур. В противном случае Верхняя доля или Ibhbyf yfrkjyf относятся к невозмущенному базовому периоду текстуры.
- Верхняя фракция
Доля ширины, приходящаяся на верхнюю поверхность.
- Ширина уклона
Доля ширины, приходящаяся на наклонные грани. Грани добавляются к верхней поверхности, но не заменяют её. Следовательно нулевая Доля верхней фракции и ненулевой наклон будет приводить к треугольным профилям.
- Асимметрия
Распределение ширины уклона для левых и правых кромок. Минус один означает что левые кромки будут наклонными и правые острыми. Плюс один означает что левые будут острыми и правые наклонными. Ноль обозначает симметричные уклоны.
Амфитеатр имеет следующие особые параметры:
- Параметр суперэллипса
Контуры ступени это суперэллипсы, описываемые уравнением где p. Нулевое значение соответствует квадратам, максимальное значение, равное двум, соответствует ромбам, значение по умолчанию, равное единице, соответствует кругам.
- Ширина террасы
Ширина одной ступени, заданная в пикселях, но также отображаемая в физических единицах. Все остальные размеры в горизонтальной плоскости задаются как доля этой базовой ширины.
Ширина включает в себя ширину наклонной части и может рассматриваться как «период» текстуры.
- Разброс положения
Случайное положение кромки ступени. Кромки никогда не пересекаются. Даже для максимального уровня случайности, они могут максимум коснуться края следующей ступени.
- Параболичность
Положительные значения означают, что терраса становится уже с увеличением расстояния от центра и весь профиль становится ближе к параболическому. Отрицательные значения приводят к обратному эффекту, общая форма становится параболой, лежащей на боку.
- Ширина уклона
Доля ширины, занятая наклонной кромкой. нуль означает острые ступени, единица означает, что текстура будет конусом (без рандомизации или влияния других модифицирующих параметров).
Концентрические окружности имеют следующие особые параметры:
- Параметр суперэллипса
Контуры колец это суперэллипсы, описываемые уравнением где p. Нулевое значение соответствует квадратам, максимальное значение, равное двум, соответствует ромбам, значение по умолчанию, равное единице, соответствует кругам.
- Период
Период текстуры, заданный в пикселях, но также отображаемый в физических единицах. Все остальные размеры в горизонтальной плоскости задаются как доля этой базовой ширины.
Поскольку эта текстура является радиальной, период надо рассматривать как отсчитываемый при движении по радиусу от центра наружу.
- Разброс положения
Рандомизация ширины отдельных пар гребень-желоб.
- Параболичность
Положительные значения означают, что терраса становится уже с увеличением расстояния от центра и весь профиль становится ближе к параболическому. Отрицательные значения приводят к обратному эффекту, общая форма становится параболой, лежащей на боку.
- Масштабировать особенности с шириной
Если включено, то все горизонтальные размеры масштабируются пропорционально ширине каждой отдельной пары гребень-впадина для рандомизированных текстур. В противном случае Верхняя доля или Ibhbyf yfrkjyf относятся к невозмущенному базовому периоду текстуры.
- Верхняя фракция
Доля ширины, приходящаяся на верхнюю поверхность.
- Ширина уклона
Доля ширины, приходящаяся на наклонные грани. Грани добавляются к верхней поверхности, но не заменяют её. Следовательно нулевая Доля верхней фракции и ненулевой наклон будет приводить к треугольным профилям.
- Асимметрия
Распределение ширины наклонов между левой и правой кромкой. Минус один означает, что внутренние кромки будут наклонными и внешние острыми. Плюс один делает внутренние острыми и внешние наклонными. Нулевое значение задаёт одинаковые наклоны в обе стороны.
Звезда Сименса имеет следующие особые параметры:
- Количество секторов
Число круговых секторов, на которые делится плоскость. Каждый сектор содержит верхнюю и нижнюю поверхность, так что количество кромок будет удвоенным числом секторов.
- Верхняя фракция
Доля углов, приходящаяся на верхнюю поверхность.
- Сдвиг края
Сдвиг кромки по отношению к радиальным ступицам, собирающимся вместе в центре. Положительные значения означают что верхняя поверхность увеличивается при сдвиге, отрицательные увеличивают нижнюю поверхность. Сдвиг не меняет асимптотическую долю верхней поверхности (для радиуса, стремящегося к бесконечности), но он меняет центр текстуры.
Прямоугольные отверстия имеют следующие особые параметры:
- Период по X и период по Y
Горизонтальный и вертикальный периоды текстуры, задаваемые в пикселях, но также отображаемые в физических единицах измерения. Все остальные пространственные размеры задаются как доля от меньшего из этих двух размеров.
- Разброс положения
Случайный выбор положения отверстий по отношению к центру прямоугольника.
- Верхняя фракция по X и Верхняя фракция по Y
Доля ширины занятой верхней поверхностью на горизонтальных и вертикальных профилях, проходящих через центр отверстия. Поскольку размеры задаются как две доли, соотношение сторон отверстия масштабируется пропорционально двум соответствующим периодам.
Верхняя грань обычно имеет большую площадь поскольку некоторые профили не пересекают отверстий – и может ещё больше увеличиваться за счёт скругления углов.
- Ширина уклона
Доля размера (меньшей стороны базового прямоугольника) занимаемая наклонными гранями. Наклон будет одинаковым в обоих направлениях.
Наклоны добавлены к верхней поверхности, они её не заменяют. Следовательно, нулевая верхняя поверхность и ненулевой наклон приводят к треугольным профилям.
- Округлость
Радиус закругления углов, задаваемый как доля размера (меньшей стороны базового прямоугольника).
Колонны имеют следующие особые параметры:
- Форма
Форма основания колонны, которая может быть круглой, квадратной или гексагональной.
- Период по X и период по Y
Горизонтальный и вертикальный периоды текстуры, задаваемые в пикселях, но также отображаемые в физических единицах измерения. Все остальные пространственные размеры задаются как доля от меньшего из этих двух размеров.
- Разброс положения
Случайный выбор положения колонн по отношению к центру прямоугольника.
- Размер
Ширина колонны, заданная как доля размера (меньшей стороны базового прямоугольника). Колонны симметричны и их соотношение сторон не масштабируется вместе с прямоугольником.
- Ширина уклона
Доля размера (меньшей стороны базового прямоугольника) занимаемая наклонными гранями. Наклон будет одинаковым в обоих направлениях.
Наклоны добавлены к верхней поверхности, они её не заменяют. Следовательно, нулевая верхняя поверхность и ненулевой наклон приводят к треугольным профилям.
- Ориентация
Поворот отдельных колонн по отношению к прямоугольной базовой решетке. Например, квадратные колонны в базовой ориентации будут выглядеть похоже на текстуру отверстий (только инвертированную), в то время как они же, но повернутые на 45 градусов образуют шахматную текстуру.
Двойная лестница имеет следующие особые параметры:
- Ширина террасы по X width и Ширина террасы по Y
Ширина и высота одной ступени в горизонтальном и вертикальном направлениях, задаваемая в пикселях, но также отображаемая в физических единицах длины. Может рассматриваться как «периоды» текстуры.
Модель вертикального роста плёнок (колоннами) использует простой механизм осаждения на основе алгоритма Монте-Карло, в котором малые частицы падают на поверхность с направлений, заданных нижеуказанными параметрами, прилипают к поверхности вблизи точки падения и увеличивают там локальную высоту. Эффект затенения при этом заставляет больше частиц прилипать к более высоким точкам поверхности, и меньше к более низким. Положительная обратная связь по высоте приводит к образованию колонн. Алгоритм рассматривает горизонтальную плоскость, заполненную идентичными копиями текущей поверхности, следовательно, генерируемые поверхности также будут периодическими (т.е. идеально сшиваться на границах). У генератора поверхности есть следующие параметры:
- Покрытие
Среднее число частиц, генерируемых над каждым пикселем поверхности.
- Высота
Увеличение локальной высоты при прилипании частицы к поверхности. Поскольку горизонтальный размер частицы всегда один пиксель, высота измеряется в пикселях. Высота в один пиксель подразумевает кубические частицы, пока рассмотрение касается процесса роста. С точки зрения детекции столкновений частицы считаются бесконечно малыми.
- Наклон
Центральный угол наклона, с которым генерируются частицы (угол падения). Нулевое значение обозначает, что малые углы падения имеют наивысшую вероятность. Большие значения означают, что частицы более вероятно упадут с большего угла, чем с меньшего. Но для большого разброса направлений, распределение остаётся изотропным в горизонтальной плоскости.
- Направление
Центральное направление в горизонтальной плоскости, с которым генерируются частицы. Большой разброс означает изотропное распределение в горизонтальной плоскости; для малых дисперсий рост анизотропен.
- Релаксация
Метод определения пикселя, к которому в конечном итоге прилипнет частица. На данный момент доступны два варианта. При слабой релаксации рассматриваются только два пикселя: непосредственно перед столкновением и после него, частица прилипает к более низкому из них. В случае сильной релаксации дополнительно рассматривается локальная область 3×3 пикселя. Частица может переместиться к более низкому соседнему пикселю с определённой вероятностью перед тем, как прилипнет насовсем к поверхности.
Вертикальное баллистическое осаждение это одна из простейших фундаментальных моделей роста плёнок. Частицы падают вертикально в произвольно выбранное место (пиксель). Высота этого места увеличивается на высоту частицы. Однако, если новая высота окажется меньше высоты любого из четырёх соседних мест, частица считается прилипшей к соседней колонне. Таким образом, высота точки падения становится равной максимальной из окружающих высот. Это является единственным механизмом, вводящим корреляции в горизонтальной плоскости в результирующую шероховатость.
Расчёт имеет всего несколько параметров:
- Покрытие
Среднее число частиц, генерируемых над каждым пикселем поверхности.
- Высота
Увеличение локальной высоты, которое происходит при падении частицы на пиксель.
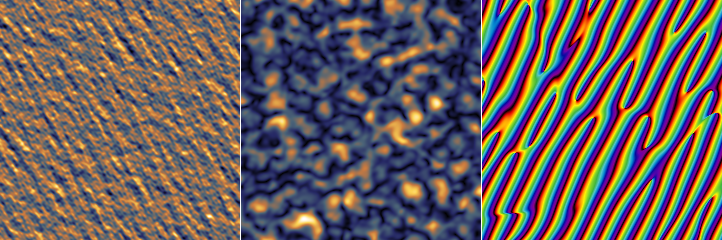
Метод волнового синтеза генерирует изображение на основе интерференции волн от набора точечных источников. Помимо обычной косинусоидальной волны, доступны несколько других форм волны, каждая из которых имеет чётный и нечётный вариант, различающиеся на сдвиг фазы π/2 во всех частотных компонентах. Когда волна рассматривается как комплексная, чётная часть (косинусоида) образует действительную часть, а нечётная (синусоида) образует мнимую.
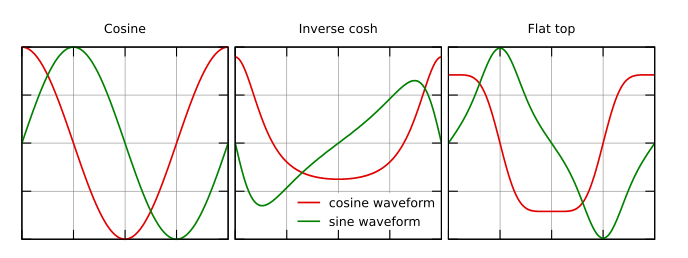
Чётные и нечётные формы волны для различных доступных видов волн. Для изображений смещения используются только косинусоидальные формы; полная комплексная волна используется для генерации изображений интенсивности и фазы.
Для генератора доступны нижеследующие опции:
- Величина
Величина для показа на изображении. Смещение это сумма действительных частей. Амплитуда это модуль комплексной волны. Фаза это фазовый угол комплексной волны.
- Число волн
Число точечных источников, от которых распространяются волны.
- Форма волны
Одна из описанных выше форм волны.
- Амплитуда
Приблизительная амплитуда высот (среднеквадратичное отклонение) генерируемого изображения. Следует отметить, что она отличается от от амплитуды отдельных волн: амплитуда высот в сгенерированном изображении должна расти пропорционально квадратному корню из числа волн в этом случае, в то время как она фактически остаётся почти постоянной пока не меняется амплитуда.
- Частота
Пространственная частота волн. Измеряется относительно размера изображение, т.е. значение 1.0 означает длину волны, равную размеру стороны изображения.
- X центра, Y центра
Координаты точечных источников. Нуль соответствует центру изображения. Координаты измеряются в размерах изображения. В общем случае, хотя бы один из соответствующих разбросов должен быть ненулевым, иначе все точечные источники будут совпадать (хотя можно сгенерировать некоторые интересные текстуры варьируя частоты).
- Затухание
Затухание определяет как быстро волны ослабляются. Значение измеряется в обратных длинах волн и задаётся как десятичный логарифм, что показывается единицами измерения log₁₀.
Расчёт реализует гибридную неравновесную модель Изинга [2], совмещающую дискретную модель Изинга для малых расстояний с непрерывным медленным ингибитором.
Дискретная переменная u имеет два возможных значения, которые она меняет с вероятностью
где ΔE – изменение энергии в результате смены состояния и T – температура. Энергия задаётся числом соседей в противоположном состоянии в направлениях вдоль координатных осей no, числом соседей в противоположном состоянии в направлении по диагоналям nd и также смещением, вызванным полем ингибитора v:
Непрерывное поле ингибитора v задано локальным дифференциальным уравнением, связанным с переменной u:
где μ – связь ингибитора и ν – параметр смещения. Граничные условия для расчёта периодические, следовательно, генерируемые изображения также будут периодическими (т.е. идеально совмещаться друг с другом на границе).
Расчёт управляется следующими параметрами:
- Число шагов
Одна итерация расчёта состоит из четырёх шагов: обновление u методом Монте-Карло, шаг по времени в решении дифференциального уравнения для v, другой шаг Монте-Карло и ещё один шаг по времени в дифференциальном уравнении. Показываемые значения v соответствуют второму обновлению. Значение, показываемое как u это среднее из двух значений, наиболее близких по времени к соответствующему значению v. Таким образом, изображения u трёхзначные, а не двузначные.
- Температура T
Температура определяет вероятность, с которой переменная с двумя состояниями u может переходить из одного в другое с энергией большей или равной (смена состояния, которая сильно понижает энергию, происходит сама по себе). Большая температура означает меньшее разделение между двумя доменами u.
- Сила ингибитора B
Сила, с которой непрерывная переменная смещает энергию в каждом пикселе. Для больших значений ингибитор играет большую роль по сравнению с поверхностным натяжением.
- Связь ингибитора μ
Фактор связи между u и v в дифференциальном уравнении для v.
- Смещение ν
Смещение в дифференциальном уравнении для v в сторону больших или меньших значений.
- Временной шаг метода Монте-Карло
Временной шаг в дифференциальном уравнении, соответствующий одному шагу в методе Монте-Карло. Таким образом, этот параметр определяет относительную скорость двух этих процессов.
- Высота
Диапазон значений создаваемых изображений.
Вкладка Предустановки содержит несколько загружаемых наборов параметров, которые генерируют интересные структуры. Можно выбрать набор предустановок и нажать чтобы загрузить набор параметров для данного генератора. Начальное число для генератора случайных чисел не является частью предустановок. Следовательно, для каждого начального числа получаемые изображения будут всё ещё варьироваться, но будут сохранять одинаковый общий облик (несколько зависит от удачи экспериментатора, некоторые случайные значения генерируют менее интересные изображения по сравнению с другими).
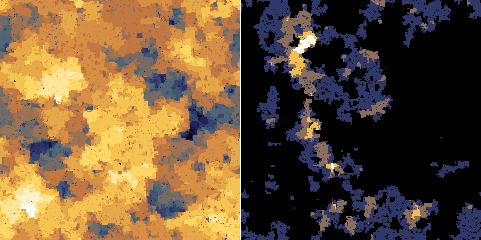
Модуль реализует простую модель клеточного автомата описывающего разделение фаз с помощью отжига не смешивающегося решеточного газа, состоящего из двух компонент A и C. Рассматривается только взаимодействие между ближайшими соседями. Различие в энергиях образования
определяет предпочтение в разделении фаз. Отжиг происходит путём обмена местами двух соседних ячеек (пикселей). релаксация всегда происходит в сторону более энергетически выгодного расположения, однако они также могут переключаться в сторону менее выгодного с вероятностью, задаваемой температурой T
Поскольку вероятность зависит только от соотношения компонент, можно задать постоянную Больцмана равной единице и тогда модель зависит только от безразмерной температуры и относительного соотношения двух компонент.
Расчёт управляется следующими параметрами:
- Число шагов
Одна итерация соответствует тому, что каждая пара расположений в соседних ячейках однократно проверяется на возможность замены. Однако, это сохраняется только в вероятностном смысле. Некоторые расположения могут быть проверены несколько раз в течение одной итерации, другие ни разу.
- Начальная температура
Безразмерная температура определяет вероятность с которой ячейки могут меняться в сторону менее энергетически выгодной конфигурации, как описано выше. Начальная температура это температура при которой начинается отжиг.
- Конечная температура
Безразмерная температура при которой моделирование завершается.
- Доля компонента
Доля компонента C в смеси A-C.
- Высота
Диапазон значений создаваемых изображений.
- Число шагов усреднения
Выводимое изображение может захватывать только финальное состояние или оно может быть расчитано усреднением определенного числа состояний до конечного, задаваемого этим параметром.
Опционально может быть задействована трёхкомпонентная модель. Третий компонент B ведёт себя подобно A и С. Однако, модель в этом случае будет содержать больше параметров:
- Доля компонента B
Доля компонента B в смеси. Остаток будет поделен между A и С в соответствии с Долей компонента.
- Энергия смешивания AB
Разница в энергиях формирования для компонент A и B по отношению к максимальному значению.
- Энергия смешивания AC
Разница в энергиях формирования для компонент A и C по отношению к максимальному значению.
- Энергия смешивания BC
Разница в энергиях формирования для компонент B и C по отношению к максимальному значению.
Для того, чтобы безразмерная температура масштабировалась одинаково с двухкомпонентной моделью, наибольшая энергия смешивания всегда нормируется к 1. Если вы пытаетесь её уменьшить, две другие энергии смешивания увеличиваются вместо неё, сохраняя соотношение, до тех пор, пока одна из них не достигнет значения 1. Тогда эта разница энергий станет наибольшей и наибольшая до этого может уменьшаться дальше.
Большое число интересных текстур может создаваться с помощью численного решения связанных нелинейных дифференциальных уравнений в частных производных в плоскости изображения. В настоящее время модуль реализует два генератора с общими основными параметрами:
- Число шагов
Число шагов по времени для решения связанных дифференциальных уравнений в частных производных. Решение практически перестаёт меняться после определенного числа итераций, которое, однако, очень сильно варьируется в зависимости от типа текстуры и её параметров.
Генератор текстуры Тьюринга может генерировать одиночную классическую текстуру в относительно управляемом режиме. Он имеет следующие параметры:
- Размер
Характеристические ширины полос в текстуре.
- Степень хаоса
Специальный параметр, управляющий сходимостью решения. Малые значения приводят к более упорядоченным текстурам. Однако, решение может сходиться очень долго для больших раземеров изображения. Большие значения приводят к более возмущенным текстурам, однако, гораздо быстрее.
Текстура генерируется двухкомпонентной моделью диффузия-реакция, с уравнениями для обоих компонентов в форме
В уравнении для второго компонента роли просто меняются (и отличаются константы). Функция f определяется как
Константы p, q и r не управляются напрямую. Они (и шаг по времени) рассчитываются из размера и степени хаотичности в соответствии с калибровочной формулой.
Модель диффузии-реакции может генерировать большое разнообразие текстур. Однако, прямая настройка скоростей реакции и параметров, таких как размер особенностей, невозможна. Модуль содержит следующие параметры:
- Тип вывода
Какой из двух компонент будет отрисовываться на изображении.
- Скорость удаления
Константа скорости реакции, относящаяся к удалению материала.
- Скорость питания
Константа скорости притока (питания) материала в реакции.
- Плотность источника
Плотность на пиксель фиксированных источников с высоким/низким значениями. Плотность рассчитывается на пиксель, множитель 10-3 не используется.
- Количество итераций без источника
Как много итераций в конце будет проводиться после того, как источники будут убраны. Можно задать значение больше, чем общее количество итераций, но это не очень полезно (при таком задании источники будут убраны с самого начала).
В большей части диапазонов параметров реакции требуется источник реагентов чтобы получались интересные текстуры. Без такого источника состояние системы развивается в постоянное плоское изображение или нестабильность в формате шахматной доски. Одной из возможностей стимулирования генерации интересных текстур (часто используемой в демонстрациях) является большая пространственная неоднородность констант реакции в области протекания. Однако, это не позволяет рассчитывать заданные специфичные текстуры для определенных наборов параметров.
Тогда, вместо этого, модуль добавляет явно заданные источники. Они реализованы в грубой форме как случайные пиксели, которые сохраняют свои низкие/высокие значения (и иногда их можно наблюдать в анимации эволюции). На них не действует реакция, но они влияют на своих ближайших соседей.
Некоторые текстуры будут стабильны после того, как они сформировались, и при удалении источников ничего не происходит. Некоторые нет и вырождаются в одно из неинтересных состояний. Немного разные наборы текстур могут быть получены при удалении источников на длительное время и при удалении источников ненадолго в конце. Кроме того, есть несколько интересных переходных текстур.
Модуль моделирования реализует дискретную модель диффузии с ограниченной агрегацией на основе метода Монте-Карло. Частицы в форме пикселей падают на поверхность и движутся вдоль неё пока не прилипают к кластеру, постепенно образуя монослой. Поток падающих частиц невелик, поэтому в каждый момент времени свободно двигается малое число частиц и частица может пройти заметное расстояние по поверхности до момента прилипания. Для типичных значений параметров это приводит к образованию кластеров в форме «фрактальной снежинки».
Расчёт управляется следующими параметрами:
- Покрытие
Среднее количество раз, когда частица попадает на заданный пиксель изображения. Значение покрытия 1 означает что поверхность будет покрыта монослоем, предполагая, что частицы покрывают её равномерно.
- Поток
Среднее число частиц, падающих на каждый заданный пиксель за один шаг моделирования. Меньшие значения потока приводят к более крупным структурам, поскольку частицы участвуют в диффузии более продолжительное время до встречи с другой частицей. Значение задано как десятичный логарифм, что показывается единицами измерения log₁₀.
- Высота
Высота отдельной частицы которая задаёт высоту ступеней в получаемом изображении.
- Вероятность прилипания
Вероятность того, что свободная частица окончательно прилипнет и перестанет двигаться, когда она касается другой отдельной частицы. Вероятности что частица прилипнет, если она коснётся двух или трёх частиц возрастает пропорционально в зависимости от этого значения. Вероятность прилипания всегда нулевая для частицы без соседей и всегда единица для частицы, окруженной четырьмя соседними.
- Вероятность активации
Вероятность для частицы, которая не прилипла что она сдвинется если она касается другой частицы. Вероятность для большего числа касающихся частиц уменьшается как степень вероятности для отдельной частицы. Частицы без соседей могут двигаться свободно всегда.
- Вероятность прохождения Швёбеля
Частица, которая упала на верхушку уже сформированного кластера может иметь сниженную вероятность спуститься на более низкий уровень из-за так называемого барьера Швёбеля. Если этот параметр равен 1, барьера нет, т.е. частицы могут свободно спускаться. Наоборот, вероятность, равная 0, означает что частицы никогда не спустятся на более низкие уровни. Значение задано как десятичный логарифм, что показывается единицами измерения log₁₀.
Следует отметить, что некоторые комбинации параметров, а именно очень маленький поток и очень низкая вероятность преодолеть барьер Швёбеля, могут привести к очень долгим временам моделирования.
Метод синтеза поверхности, основанный на случайном размещении волокон сильно похож на метод синтеза Объекты, за исключением того, что вместо объектов ограниченного размера он добавляет бесконечно длинные (в принципе) волокна на поверхность.
Генератор имеет небольшой набор параметров, поделенных между вкладками Генератор и Размещение. Первая группа содержит основные настройки и параметры, определяющие профили отдельных волокон:
- Форма
Форма профиля поперёк волокна. Опции Полукруг, Треугольник, Прямоугольник и Парабола не требуют пояснений. Форма Квадратичный сплайн соответствует кусочной квадратичной функции, состоящей из трёх частей, которая является базисной функцией квадратичного B-сплайна.
- Покрытие
Среднее количество волокон перекрывающих один пиксель изображения. Значение покрытия 1 означает что поверхность будет ровно один раз покрыта волокнами, при этом они будут покрывать её равномерно и не будут пересекаться. Большие значения означают больше слоёв объектов и более медленную генерацию изображения. Значение является приблизительным и действительное покрытие немного зависит от других параметров.
- Ширина
Ширина волокна в пикселях. Также имеет обычную связанную опцию Разброс, которая определяет различия между отдельными волокнами. Однако, для волокон ширина также может меняться вдоль каждого отдельного волокна. Это настраивается опцией Вдоль волокна. Высокие значения разброса вдоль волокна могут в сочетаниях с некоторыми другими опциями (в частности, высокими значениями деформации по длине и высокими значениями разброса толщины) приводить к странно выглядящим изображениям и возможным артефактам.
- Высота
Величина, пропорциональная высоте волокна, обычно высота наивысшей точки. Также как и Ширина, она имеет два разброса, между отдельными волокнами и вдоль каждого индивидуального волокна.
Выбор опции Масштабируется с шириной заставляет невозмущённые высоты масштабироваться пропорционально ширине волокна. В противном случае высота не зависит от размера.
Кнопка как у текущего изображения устанавливает значение высоты равным значению, основанном на среднеквадратичном отклонении текущего изображения.
- Усечение
Волокна могут быть усечены на определённой высоте для создания профилей в форме усечённых полукругов, парабол, и т.п. Высота усечения задаётся в долях от общей высоты объекта. Единица означает неусечённую фигуру, ноль – полное удаление волокна.
Вторая группа содержит опции, управляющие тем, как волокна деформируются и добавляются к изображению:
- Ориентация
Поворот волокон, измеренный против часовой стрелки. Ноль соответствует ориентации слева направо.
- Плотность
Плотность управляет тем, как часто волокно деформируется по его длине. Низкая плотность соответствует постепенной деформации на больших масштабах, в то время, как высокая плотность означает что волокно деформируется часто, что приводит к волнистым и извилистым формам.
- Горизонтальный масштаб
Как сильно волокно деформировано в направлении, перпендикулярном его основному направлению. Увеличение этого значения делает волокно извилистым, правда в относительно правильной форме.
- По длине
Как сильно точки волокна смещаются вдоль его длины. Увеличение этого параметра вызывает появление неправильных перекручиваний и петель (или даже узлов).
Модуль синтеза решеток создаёт поверхности основанные на случайных двумерных решетках. Он содержит две основные части. В первой, управляемой параметрами во вкладке Решетка, создаётся набор точек в плоскости, которые организованы в более или менее случайную решетку. Вторая часть, управляемая параметрами во вкладке Поверхность, создаёт реальную поверхность, основанную на величинах, рассчитанных в ходе тесселяции Вороного и /или триангуляции Делоне для заданного набора точек.
Создание решетки управляется следующими параметрами:
- Решетка
Основной тип решетки. Случайная решетка соответствует полностью случайно расположенным точкам. Другие типы соответствуют правильному расположению точек (квадратному, гексагональному, треугольному), хорошо известным мозаичным заполнениям (каирской, плосконосой квадратной, Пенроуза) или восстановлениям поверхности (кремний 7×7).
- Размер
Средний размер ячейки. Точнее, этот параметр описывает среднюю плотность точек. Он равен стороне квадрата, если такое же число точек организовано в квадратную решетку.
- Релаксация решетки
Величина, на которую решетке можно релаксировать. Процесс релаксации отталкивает точки от очень близких соседей в сторону большой пустой области. В целом это приводит к тому, что размеры ячеек становятся более равномерными. Естественно, процесс релаксации не влияет на правильные решетки. Следует отметить, что релаксация требует прогрессивной ретесселяции и большой параметр релаксации может существенно замедлить генерацию поверхности.
- Релаксация высоты
Величина, на которую могут релаксировать случайные значения, присвоенные каждой точке (см. ниже). Процесс релаксации похож на диффузию и приводит к общему сглаживанию случайных значений.
- Ориентация
Поворот решетки по отношению к определённому исходному направлению, измеренный против часовой стрелки. Доступно только для правильных сеток, поскольку случайная сетка является изотропной.
- Амплитуда, Горизонтальный масштаб
Параметры, управляющие деформацией решетки. Имеют то же значение, что и в синтезе структур.
Финальная поверхность строится как взвешенная сумма набора основных величин, полученных в результате тесселяции Вороного или триангуляции Делоне. Каждая величина может быть включена или выключена. Если она выбрана в списке, её вес добавляется к сумме и её пороговые параметры можно модифицировать двигая ползунки. Нижний и верхний порог ограничивают диапазон значений (который всегда нормализован до [0, 1]) меняя все величины выше верхнего порога на величину порога и аналогично для нижнего.
Некоторые из основных величин рассчитываются только из горизонтальных координат. Некоторые, однако, рассчитываются из случайных значений («высот»), присвоенных каждой точке множества. Доступные величины включают в себя:
- Случайная постоянная
Округляющая интерполяция между случайными величинами, присвоенными каждой точке множества. Это означает, что каждая ячейка Вороного заполнена постоянной случайной величиной.
- Случаная линейная
Линейная интерполяция между случайными величинами, присвоенными каждой точке множества. Следовательно, поверхность является непрерывной и каждому треугольнику Делоне соответствует грань поверхности.
- Случайная выпуклая
Интерполяция похожа на предыдущую, но является нелинейной, создавая относительно ровные области вокруг каждой точки множества.
- Радиальное расстояние
Расстояние до ближайшей точки множества.
- Сегментированное расстояние
Расстояние до ближайшей границы ячейки Вороного, масштабированное в каждом сегменте ячейки таким образом, чтобы точка множества была равноудалена от всех границ.
- Сегментированное случайное
Та же величина, что и сегментированное расстояние, но умноженная на случайное значение, присвоенное точке множества.
- Расстояние до границы
Расстояние до ближайшей границы ячейки Вороного.
- Случайное до границы
Та же величина, что и расстояние до границы, но умноженная на случайную величину, присвоенную точке множества.
- Расстояние до второго ближайшего
Расстояние до второй ближайшей точки множества.
Этот модуль генерирует, помимо других вещей, поверхности с профилями, подобными дробному броуновскому движению. Метод создания, однако, не очень сложен. Начиная от углов изображения, внутренние точки рекурсивно линейно интерполируются вдоль горизонтальной и вертикальной осей, добавляя шум, который масштабируется с расстоянием согласно заданной экспоненте Хёрста. Некоторые из поверхностей окажутся такими же, как генерирует спектральный синтез, однако, создание их в линейном пространстве, а не в пространстве частот, позволяет менять их различные свойства.
Генератор настраивается нижеследующими параметрами:
- Экспонента Хёрста
Экспонента Хёрста H. Для нормальных значений между 0 и 1, квадратный корень из функции корреляции высота-высота растёт как H-тая степень расстояния. Алгоритм создания позволяет использовать даже отрицательные значения, поскольку он останавливается при конечном разрешении в один пиксель.
- Масштаб стационарности
Масштаб, на котором принудительно реализуется стационарность (следует заметить, что дробное броуновское движение не является стационарным). Когда этот масштаб сравним с размером изображения или больше, он оказывает немного влияния. Однако, когда он мал, изображение становится «усреднённым» вместо самоподобия выше этого масштаба.
- Распределение
Распределение шума, добавленного при генерации. Равномерный и гауссов приводят в общем случае к одинаковым поверхностям (статистически); первый, однако, является более быстрым. Более тяжелые в хвосте распределения, т.е. экспоненциальное и особенно степенное, приводят к ярко выраженным пикам и впадинам.
- Степень
Степень α степенного распределения. Функция плотности вероятности пропорциональна
- Ср. квадр.
Среднеквадратичное значение высот (или отличий от средней плоскости, которая, однако, всегда является плоскостью z = 0). Следует отметить, что это значение применяется к данному генерируемому изображению, не процессу как таковому, который не имеет конечного среднеквадратичного отклонения. Кнопка Как у текущего изображения устанавливает значение среднеквадратичного отклонения равным ему же для текущего изображения.
Модуль создаёт данные несколько напоминающие структуру магнитных доменов, изучаемых магнитно-силовой микроскопией (МСМ) или структуру полимеров в органических солнечных батареях, изучаемую каким-либо видом контрастирования состава (ИК, КР, силовые кривые). В отличие от более физически правильных, но требующих больших вычислительных ресурсов подходов, данный работает на основе спектрального синтеза поверхности с ограниченным набором пространственных частот и последующем применении морфологических операций для получения изображений двух фаз. Выходное изображение в данном методе в основном состоит из двух значений, соответствующих двум фазам, хотя иногда может появляться промежуточное «переходное» значение.
Генератор настраивается нижеследующими параметрами:
- Размер
Типичная ширина полосы.
- Разброс размеров
Разброс размеров (или. точнее, пространственных частот). Малый разброс означает гладкие правильные элементы структуры. Однако, для очень малых значений разброса на изображении могут появиться предпочтительные направления (и оно станет анизотропным) вследствие исчерпания набора допустимых пространственных частот. Большой разброс означает менее правильные границы раздела фаз и большее количество переходных областей.
- Высота
Различие в значениях соответствующих двум различным фазам, определяет общий масштаб изображения по z.
Модуль создаёт данные, состоящие из непересекающихся дисков, возможно постобработанных таким образом, чтобы образовать поверхность, покрытую черепицей (мозаичной текстурой). Подобного результата можно также достичь используя синтез Объектов если включена опция Избегать наложения. Однако, в данном случае, только несколько затравочных дисков расположены случайным образом, остальные всегда помещаются в центр самого большого оставшегося пустого пространства. Это приводит к более равномерному распределению размеров. Более того, преобразование в черепицу создаёт структуру, где обычно три объекта встречаются под углами близкими к 120 градусам, подобно пенистым структурам.
Генератор настраивается нижеследующими параметрами:
- Начальный радиус
Радиус диска-затравки, случайно размещаемого в начале.
- Минимальный радиус
Минимально допустимый радиус всех остальных дисков. Когда не остаётся места для диска хотя бы такого размера, генерация останавливается.
- Зазор
Дополнительный отступ от соседних дисков. В то время, как Минимальный радиус задаёт минимальный размер действительно размещаемых дисков, этот параметр увеличивает минимальный размер свободного пространства, куда можно поместить диск.
- Преобразовать в мозаику
Если включено, все диски расширяются до того момента, как они начнут касаться своих соседей. Поверхность становится мозаичной, с тонкими зазорами между отдельными фрагментами.
- Толщина зазора
Ширина зазора между элементами мозаики после преобразования.
- Применить фильтр размыкания
Если включено, мозаичное покрытие затем подвергается обработке фильтра размыкания заданного размера. Этот процесс убирает слишком маленькие детали и делает оставшиеся более округлыми.
- Размер
Размер фильтра размыкания.
- Высота
Высота дисков или мозаики по отношению к базовому уровню, определяет общий масштаб оси z изображения. Высоты отдельных особенностей будут распределены вокруг этого значения когда параметр Разброс ненулевой.
Модуль основан на простом моделировании формирования ветровых дюн [3]. Частицы могут быть подхвачены ветром с определенной вероятностью, перенесены вдоль направления ветра и осесть в новом месте. Функция имеет следующие параметры:
- Покрытие
Среднее число частиц на единичный пиксель.
- Число шагов
Одна итерация соответствует тому, что ветер подхватывает одну случайную частицу в каждом пикселе и она осаждается где-то ещё. Однако, пиксели при этом выбираются случайно. Некоторые места могут быть выбраны несколько раз в ходе одной итерации, другие ни разу. Некоторые из выбранных мест могут быть голой скалой-основанием на которой нет песчаных частиц чтобы их подхватить.
- Направление и Разброс
Среднее направление ветра и разброс этого направления. Малый разброс соответствует случаю, когда направление ветра постоянно. Большие значения соответствуют более случайному направлению ветра.
- Минимальный шаг и Диапазон шагов
Песчаная частица может считаться касающейся поверхности временами и переносимой ветром высоко над поверхностью между касаниями. Она может осесть на поверхность когда она касается её. Минимальный шаг это минимальное расстояние (в пикселях) одного такого скачка; диапазон задаёт интервал (снова в пикселях) между минимальной и максимальной длиной прыжка.
- Вероятность прилипания на скалах
Вероятность частицы осесть на поверхность когда она касается голой скалы.
- Вероятность прилипания на песке
Вероятность частицы осесть на поверхность когда она касается поверхности и там уже есть некоторое количество песка. Эта вероятность в общем случае должна быть выше, чем для голой скалы.
- Максимальный уклон
Когда осаждение частицы (или подхватывание её ветром) создаёт слишком большую разницу высоты между соседними пикселями песок становится нестабильным. Он после этого сползает вниз чтобы либо уменьшить высоту холма, либо заполнить впадины пока максимальный уклон нигде не будет превышен.
Поверхность создается наложением хлопьев или плато поверх друг друга, начиная с наибольшего и двигаясь к меньшему в соответствии с законом масштабирования. По умолчанию они не пересекаются, но можно включить режим наложения хлопьев (немного похоже на то, как происходит с одномерными материалами по типу графена). Генератор использует следующий набор параметров:
- Максимальный размер
Приблизительный максимальный радиус плато.
- Минимальный размер
Приблизительный минимальный радиус плато.
- Степенной закон размера
Насколько быстро радиус плато уменьшается с увеличением количества уже помещенных плато. Большие значения означают то, что размер быстро убывает и плато имеют тенденцию быть редкими и изолированными. Малые значения означают что размер убывает медленно и плато имеют тенденцию быть плотными и складываться в высокие структуры.
Предупреждение
Может быть сложно, или даже невозможно, найти положения всех плато с заданным максимальным и минимальным размером и степенью масштабирования. Низкие степени полезны только с узкими диапазонами размеров. В противном случае генератор поверхности будет очень медленным или вообще никогда не закончит работать.- Неправильность формы
Насколько сильно формы могут отклоняться от симметричных дисков.
- Степень пересечения
Приблизительная доля плато, которые будут пересекаться с другими плато.
- Масштабируется со степенью размера
Степень, с которой высота плато масштабируется с его размером. Для заданной по умолчанию степени 0 все плато будут иметь одинаковую высоту (за исключением возможного случайного разброса). Положительные степени означают, что высота уменьшается с уменьшением размера. Отрицательные степени означают, что более маленькие плато будут выше, создавая поверхность с пиками.
Смачивание это простое моделирование движения границы смачивания через случайную среду. Среда представлена сеткой вокселей, где каждый воксель имеет разное сопротивление. Жидкость всегда распространяется через воксель с минимальным сопротивлением. Генератор создает изотропные текстуры с дискретной высотой, соответствующей уровням, до которых дошел фронт смачивания. Генератор имеет следующий набор параметров:
- Покрытие
Среднее количество раз, которое жидкость проходит через пиксель. Результирующее изображение показывает только наиболее дальние точки, таким образом его среднее значение не связано напрямую с покрытием.
- Диффузия
Вероятность случайного распространения с соседних вокселей, не связанное с приоритетом основанным на сопротивлении. Следует отметить, что значение является логарифмическим.
[1] D. Nečas, P. Klapetek: Synthetic Data in Quantitative Scanning Probe Microscopy. Nanomaterials 11 (2021) 1746 10.3390/nano11071746
[2] L. M. Pismen, M. I. Monine, G. V. Tchernikov: Patterns and localized structures in a hybrid non-equilibrium Ising model. Physica D 199 (2004) 82, doi:10.1016/j.physd.2004.08.006
[3] B. T. Werner: Eolian dunes: Computer simulations and attractor interpretation. Geology 23 (1995) 1107, doi:10.1130/0091-7613(1995)023<1107:EDCSAA>2.3.CO;2